1  A statistical model for improved membrane protein expression using sequence-derived features

Adapted from Saladi SM, Javed N, Müller A, Clemons WM. 2018. A statistical model for improved membrane protein expression using sequence-derived features. J Biol Chem 293:4913–4927. doi:10.1074/jbc.RA117.001052

1.1 Abstract

The heterologous expression of integral membrane proteins (IMPs) remains a major bottleneck in the characterization of this important protein class. IMP expression levels are currently unpredictable, which renders the pursuit of IMPs for structural and biophysical characterization challenging and inefficient. Experimental evidence demonstrates that changes within the nucleotide or amino-acid sequence for a given IMP can dramatically affect expression levels; yet these observations have not resulted in generalizable approaches to improve expression levels. Here, we develop a data-driven statistical predictor named IMProve, that, using only sequence information, increases the likelihood of selecting an IMP that expresses in E. coli. The IMProve model, trained on experimental data, combines a set of sequence-derived features resulting in an IMProve score, where higher values have a higher probability of success. The model is rigorously validated against a variety of independent datasets that contain a wide range of experimental outcomes from various IMP expression trials. The results demonstrate that use of the model can more than double the number of successfully expressed targets at any experimental scale. IMProve can immediately be used to identify favorable targets for characterization. Most notably, IMProve demonstrates for the first time that IMP expression levels can be predicted directly from sequence.

1.2 Introduction

The biological importance of integral membrane proteins (IMPs) motivates structural and biophysical studies that require large amounts of purified protein at considerable cost. Only a small percentage can be produced at high-levels resulting in IMP structural characterization lagging far behind that of soluble proteins; IMPs currently constitute less than 2% of deposited atomic-level structures (Hendrickson, 2016). To increase the pace of structure determination, the scientific community created large government-funded structural genomics consortia facilities, like the NIH-funded New York Consortium on Membrane Protein Structure (NYCOMPS) (Punta et al., 2009). For this representative example, more than 8000 genes, chosen based on characteristics hypothetically related to success, yielded only 600 (7.1%) highly expressing proteins (Love et al., 2010) resulting to date in 34 (5.6% of expressed proteins) unique structures (based on annotation in the RCSB PDB (Berman et al., 2000)). This example highlights the funnel problem of structural biology, where each stage of the structure pipeline eliminates a large percentage of targets compounding into an overall low rate of success (Lewinson et al., 2008). With new and rapidly advancing technologies like cryo-electron microscopy, serial femtosecond crystallography, and micro-electron diffraction, we expect that the latter half of the funnel, structure determination, will increase in success rate (Johansson et al., 2017; Merk et al., 2016; Nannenga and Gonen, 2016). However, IMP expression levels will continue to limit targets accessible for study (Bill et al., 2011).

Tools are needed for improving the number of IMPs with successful heterologous expression (we use expression synonymously for the term ‘overexpression’ in the field). While significant work has shown promise on a case-by-case basis, e.g., growth at lower temperatures, codon optimization (Nørholm et al., 2012), 5’ UTR randomization (Mirzadeh et al., 2015), and regulating transcription (Wagner et al., 2008), a generalizable solution remains elusive. Several RNA structure prediction methods have been used to explain or predict soluble protein expression levels (Price et al., 2009; Reis and Salis, 2020). For individual IMPs, simple changes, can have dramatic effects on the amount of expressed proteins—only partially explained by computational methods in the case of modifications at the 5’ region (Mirzadeh et al., 2015; Sarkar et al., 2008; Schlinkmann et al., 2012). Broadly, each new IMP target must be addressed individually as the conditions that were successful for a previous target seldom carry over to other proteins, even amongst closely related homologs (Lewinson et al., 2008; Marshall et al., 2016).

Considering the scientific value of IMP studies, it is surprising that there are no methods that can provide solutions for improved expression outcomes with broad applicability across protein families and genomes. There are no approaches that can decode sequence-level information for predicting IMP expression; yet it is common knowledge that sequence changes which alter overall biophysical features of the protein and mRNA transcript can measurably influence IMP biogenesis. While physics-based approaches which have proven successful in correlating integration efficiency and expression (Marshall et al., 2016; Niesen et al., 2017), that and other work revealed that simple application of specific ‘sequence features’ are inadequate to predict IMP expression (Daley et al., 2005; Nørholm et al., 2013). As an example, while the positive-inside rule is an important indicator of proper IMP biogenesis, the number of positive-charges on cytoplasmic loops alone does not predict expression level (Seppälä et al., 2010; Van Lehn et al., 2015). The reasons for this failure to connect sequence to expression likely lie in the complex underpinnings of IMP biogenesis, where the interplay between many sequence features at both the protein and nucleotide levels must be considered. Optimizing for a single sequence feature likely diminishes the beneficial effect of other features (e.g., increasing TM hydrophobicity might diminish favorable mRNA properties). Without accounting for the broad set of sequence features related to IMP expression, it is impossible to predict differences in expression levels.

Development of a low-cost, computational resource that significantly and reliably predicts improved expression outcomes would transform the study of IMPs. Attempts to develop such algorithms have so far failed. Several examples, Daley, von Heijne, and coworkers (Daley et al., 2005; Nørholm et al., 2013) as well as NYCOMPS, were unable to use experimental expression data sets to train models that returned any predictive performance (personal communication). This is not surprising, given the difficulty of expressing IMPs and the limits in the knowledge of the sequence features that drive expression. In other contexts, statistical tools based on sequence have been shown to work; for example, those developed to predict soluble protein expression and/or crystallization propensities (Bertone et al., 2001; Jahandideh et al., 2014; Price et al., 2009). Such predictors are primarily based on available experimental results from the Protein Structure Initiative (Chen et al., 2004; Gabanyi et al., 2011). While collectively these methods have supported significant advances in biochemistry, none of the models are able to predict IMP outcomes due to limitations inherent in the model development process. As IMPs have an extremely low success rate, they are either explicitly excluded from the training process or are implicitly down-weighted by the statistical model (for representative methodology see (Slabinski et al., 2007a)). Consequently, none have successfully been able to map IMP expression to sequence.

Here, we demonstrate for the first time that it is possible to predict IMP expression directly from sequence. The resulting predictor allows one to enrich expression trials for proteins with a higher probability of success. To connect sequence to prediction, we develop a statistical model that maps a set of sequences to experimental expression levels via calculated features—thereby simultaneously accounting for the many potential determinants of expression. The resulting IMProve model allows ranking of any arbitrary set of IMP sequences in order of their relative likelihood of successful expression. The IMProve model is extensively validated against a variety of independent datasets demonstrating that it can be used broadly to predict the likelihood of expression in E. coli of any IMP. With IMProve, we have built a way for more than two-fold enrichment of positive expression outcomes relative to the rate attained from the current method of randomly selecting targets. We highlight how the model informs on the biological underpinnings that drive likely expression. Finally, we provide direct examples where the model can be used for a typical researcher. Our novel approach and the resulting IMProve model provide an exciting paradigm for connecting sequence space to complex experimental outcomes.

1.3 Results

For this study, we focus on heterologous expression in E. coli, due to its ubiquitous use as a host across the spectrum of the membrane proteome. Low cost and low barriers for adoption highlight the utility of E. coli as a broad tool if the expression problem can be overcome. Furthermore, proof-of-principle in E. coli will illustrate methodology for constructing similar predictive methods for expressing IMPs in other hosts (e.g., yeast, insect cells).

1.3.1 Development of a computational model trained on E. coli expression data

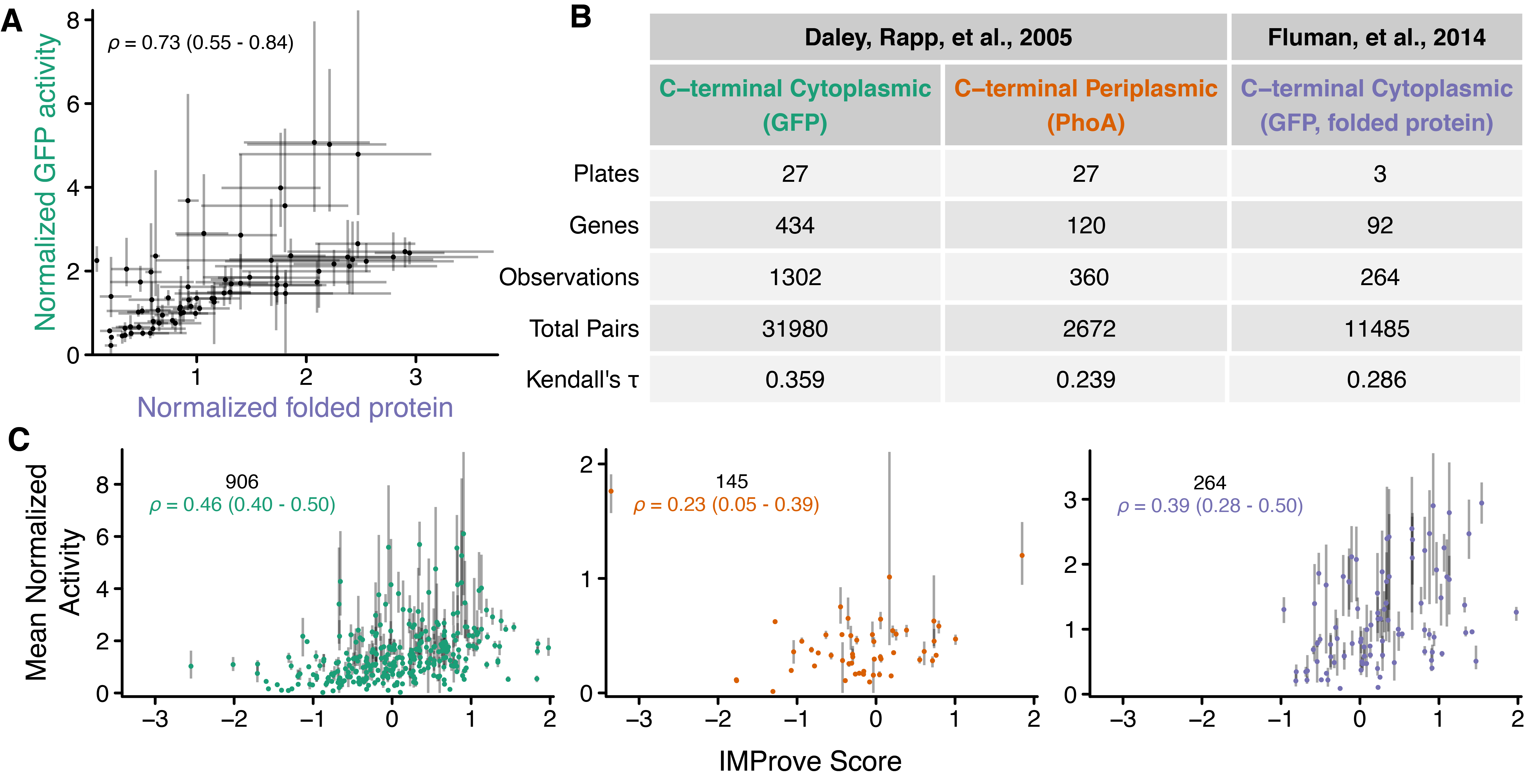
A key component of any data-driven statistical model is the choice of dataset used for training. Having searched the literature, we identified two publications that contained quantitative datasets on the IPTG-induced overexpression of E. coli polytopic IMPs in E. coli. The first set, Daley, Rapp et al., contained activity measures, proxies for expression level, from C-terminal tags of either GFP or PhoA (alkaline phosphatase)(Daley et al., 2005). The second set, Fluman et al., used a subset of constructs from the first and contained a more detailed analysis utilizing in-gel fluorescence to measure folded protein (Fluman et al., 2014) (see Section 1.5.4). The expression levels strongly correlated (Spearman’s \(\rho\) = 0.73) between the two datasets demonstrating that normalized GFP activity was a good measure of the amount of folded IMP (Figure 1.1A and (Fluman et al., 2014; Geertsma et al., 2008)). The experimental set-up employed multiple 96-well plates over multiple days resulting in pronounced variability in the absolute expression level of a given protein between trials. Daley, Rapp et al. calculated average expression levels by dividing the raw expression level of each protein by that of a control protein on the corresponding plate.

Figure 1.1: Training performance. (A) A comparison of GFP activity (Daley et al., 2005) with measured folded protein (Fluman et al., 2014) where each point represents the mean for a given gene tested in both works, and error bars plot the extrema. Spearman’s rank correlation coefficient and 95% confidence interval (CI) (Canty and Ripley, 2015) are shown. (B) Plates are the number of independent sets of measurements within which expression levels can be reliably compared. Genes are the number of proteins for which the C-terminus was reliably ascertained (Daley et al., 2005). Observations are the total number of expression data points accessible. Total pairs are the number of comparable expression measurements (i.e., those within a single plate). Kendall’s \(\tau\) is the metric maximized by the training process (See Section 1.5.4). The color of the column heading identifying each experimental set is retained throughout the figure. (C) Agreement against the normalized outcomes plotted as the mean activity (see Section 1.5.5 for definition) versus the score with error bars providing the extent of observed activities (Spearman’s \(\rho\) and 95% CI noted).

To successfully map sequence to expression, we additionally needed to derive numerical features from a given gene sequence that have been empirically related to expression. 87 sequence features from protein and nucleotide sequence were calculated for each gene using custom code together with published software (codonW (Peden, 2000), tAI (dos Reis et al., 2003), NUPACK (Zadeh et al., 2011), Vienna RNA (Lorenz et al., 2011), Codon Pair Bias (Coleman et al., 2008), Disembl (Linding et al., 2003), and RONN (Yang et al., 2005)). Relative metrics (e.g., codon adaptation index) are calculated with respect to the E. coli K-12 substr. MG1655 (Zhou and Rudd, 2013) quantity. The octanol-water partitioning (Wimley et al., 1996), GES hydrophobicity (Engelman et al., 1986), \(\Delta G\) of insertion (Hessa et al., 2007) scales were employed as well. Transmembrane segment topology was predicted using Phobius constrained for the training data and Phobius for all other datasets (Käll et al., 2004). Two RNA secondary structure metrics were prompted in part by Goodman, et al. (Goodman et al., 2013). Table 1.1 includes a detailed description of each feature. All features are calculated solely from the coding region of each gene of interest excluding other portions of the open reading frame and plasmid (e.g., linkers and tags, 5’ untranslated region, copy number).

Fitting the data to a simple linear regression provides a facile method for deriving a weight for each feature. However, using the set of sequence features, we were unable to successfully fit a linear regression using the normalized GFP and PhoA measurements reported in the Daley, Rapp et al. study. Similarly, using the same feature set and data, we were unable to train a standard linear Support Vector Machine (SVM) to predict the expression data either averaged or across all plates (see Table 1.1; Section 1.5.2, Section 1.5.3). Due to the attempts by others to fit this data, this outcome may not be surprising and suggested that a more complex analysis was required.

We hypothesized that training on relative measurements across the entire dataset introduced errors that were limiting. To address this, we instead only compare measurements within an individual plate, where differences between trials are less likely to introduce errors. To account for this, a preference-ranking linear SVM algorithm (SVM^rank (Tsochantaridis et al., 2005)) was chosen (see Section 1.5.4). Simply put, the SVM^rank algorithm determines the optimal weight for each sequence feature to best rank the order of expression outcomes within each plate over all plates, which results in a model where higher expressing proteins have higher scores. The outcome is identical in structure to a multiple linear regression, but instead of minimizing the sum of squared residuals, the SVM^rank cost function accounts for the plate-wise constraint specified above. In practice, the process optimizes the correlation coefficient Kendall’s \(\tau\) (Equation 1.1) to converge upon a set of weights.

\[ \tau_{\text{kendall}} = \frac{\text{N}_\text{correctly ordered pairs} - \text{N}_\text{swapped pairs}}{\text{N}_\text{total pairs}} \tag{1.1}\]

The SVM^rank training metric shows varying agreement for all three groups (i.e., \(\tau_{\text{kendall}} > 0\)) (Figure 1.1B). For individual genes, activity values normalized and averaged across trials were not directly used for the training procedure (see Section 1.5.4); yet one would anticipate that scores for each gene should broadly correlate with the expression average. Indeed, the observed normalized activities positively correlate with the score (dubbed IMProve score for Integral Membrane Protein expression improvement) output by the model (Figure 1.1C, \(\rho > 0\)). Since SVM^rank transforms raw expression levels within each plate to ranks before training, Spearman’s \(\rho\), a rank correlation coefficient describing the agreement between two ranked quantities, is better suited for quantifying correlation over more common metrics like the \(R^2\) of a regression and Pearson’s \(r\). While these metrics demonstrate that the model can rank expression outcomes across all proteins in the training set, for PhoA-tagged proteins, the model appears less successful. The implications for this are discussed later (see Figure 1.2G).

1.3.2 Demonstration of prediction against an independent large expression dataset

While the above analyses show that the model successfully fits the training data, we assess the broader applicability of the model outside the training set based on its success at predicting the outcomes of independent expression trials from distinct groups and across varying scales. The first test considers results from NYCOMPS, where 8444 IMP genes entered expression trials, in up to eight conditions, resulting in 17114 expression outcomes (Figure 1.2A) (Punta et al., 2009). The majority of genes were attempted in only one condition (Figure 1.2B), and, importantly, outcomes were non-quantitative (binary: expressed or not expressed) as indicated by the presence of a band by Coomassie staining of an SDS-PAGE gel after small-scale expression, solubilization, and nickel affinity purification (Love et al., 2010). For this analysis, the experimental results are either summarized as outcomes per gene or broken down as raw outcomes across defined expression conditions. For outcomes per gene, we can consider various thresholds for considering a gene as positive based on NYCOMPS expression success (Figure 1.2B). The most stringent threshold only regards a gene as positive if it has no negative outcomes (“Only Positive”, Figure 1.2B, red). Since a well expressing gene would generally advance in the NYCOMPS pipeline without further small-scale expression trials, this positive group likely contains the best expressing proteins. A second category comprises genes with at least one positive and at least one negative trial (“Mixed”, Figure 1.2B, blue). These genes likely include proteins that are more difficult to express.

Figure 1.2: Success of the model against outcomes from NYCOMPS. (A) An overview of the NYCOMPS outcomes and (B) a histogram of the number of conditions tested per gene colored based on outcome. (C) Histograms of genes with Only Positive (red) and Only Negative outcomes (grey) across IMProve scores (binned as described in Section 1.5.5). The percentage of Only Positive outcomes in each bin is overlaid as a brown line (right axis). Yellow lines indicate the 75^th (dashed) and 91^st (solid) percentiles in IMProve score (-0.2 and 0.5, respectively). (D) Receiver Operating Characteristics for positive groupings given by Only Positive outcomes genes (red) and genes with at least one positive outcome (pink). The percent positive for each group (corresponding color), total counts (black), and Area Under the Curve (AUC) values with 95% Confidence Interval (CI) are shown. The ROC considering genes with Mixed outcomes only as positive is shown as a blue dashed line with an AUC of 53.5 (51.8-55.2). The grey dashed line shows the performance of a completely random predictor (AUC = 50). (E) The AUCs for outcomes across all trials and within the most-tested plasmids along with 95% CI. Performances are also split by predicted C-terminal localization (Käll et al., 2004). The numbers below indicate the total number of trials for each group and the percent within that group that were positive. (F) The NYCOMPS dataset split by the presence or absence of a Pfam family in the training set with AUCs calculated by considering Only Positive genes as positive outcomes.

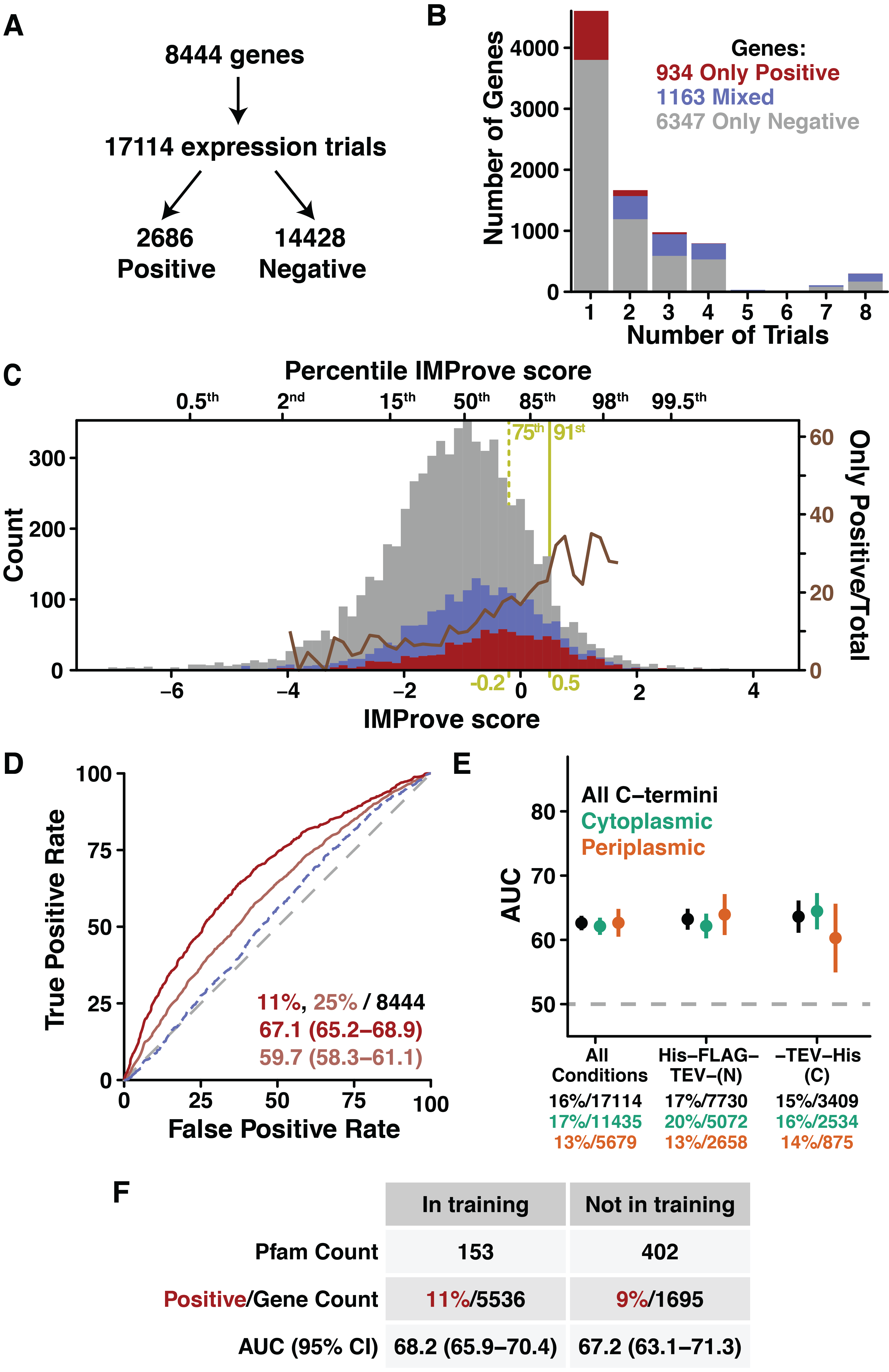
A histogram of the IMProve scores for genes separated by expression success shows predictive power of the IMProve model (Only Positive, red; Mixed, blue; Only Negative, grey) (Figure 1.2C). Visually, the distribution of the scores for the Only Positive group is shifted to a higher score relative to the Only Negative and Mixed groups. The dramatic increase in the percentage of Only Positive genes as a function of increasing IMProve score (overlaid as a brown line) further emphasizes this. In fact, simply selecting the top 25% of proteins by IMProve score (-0.2 or higher, Figure 1.2C, yellow dotted line) would have increased the number of positive outcomes from 11% to 20%, a 1.8 fold improvement.

While this is suggestive, we aim to more systematically assess predictive power. For NYCOMPS and subsequent data sets, the outcomes are either binary (e.g., in NYCOMPS expressed or not expressed) or categorical (e.g., arbitrary ranked scale), correlation coefficients cannot be used here. Instead, we turn to an alternative framework: the Receiver Operating Characteristic (ROC). ROC curves quantify the tradeoff between true positive and false positive predictions across numerical scores from a predictor. The figure of merit is the Area Under the ROC Curve (AUC), where a perfect predictor has an AUC = 100% and a random predictor has an AUC = 50 % (Figure 1.2D, grey dashed line). An AUC greater than 50% indicates that a model is predictive (percentage signs hereafter omitted) (see Section 1.5.5 and (Swets et al., 2000)). We will use the ROC framework to quantitatively validate the ability of our model to predict protein expression data—all independent of the training process.

Returning to the NYCOMPS data, ROC analysis shows that the IMProve model markedly distinguishes genes in the most stringent positive group (Only Positive) from all other genes (AUC = 67.1) (Figure 1.2C red). A permissive threshold considering genes as positive with at least one positive trial (Only Positive plus Mixed genes) shows moderate predictive power (Figure 1.2C pink, AUC = 59.7). If instead the Mixed genes are considered alone (excluding the Only Positive), the model very weakly distinguishes the Mixed group from the Only Negative genes (Figure 1.2C dashed blue, AUC = 53.5). This likely supports the notion that the Mixed pool largely consists of more difficult-to-express genes.

We next confirm the ability of the IMProve model to predict within plasmids or sequence space distinct from those within the limited training set. For an overfit model, one might expect that only the subset of targets which most closely mirror the training data would show strong prediction. On the contrary, the model shows consistent performance throughout each of the eight distinct experimental conditions tested (Figure 1.2G and Table 1.2). One may also consider that the small size of the training set limited the number of protein folds sampled and, therefore, limited the number of folds that could be predicted by the model. To test this, we consider the performance of the model with regards to protein homology families, as defined by Pfam family classifications (Finn et al., 2014). The 8444 genes in the NYCOMPS dataset fall into 555 Pfam families (~15% not classified). To understand whether the IMProve score is biased towards families present in the training set, we separate genes in the NYCOMPS dataset into either within the 153 Pfam families found in the training set or outside this pool (i.e., not in the training set). Satisfyingly, there is no significant difference in AUC at 95% confidence between these groups (68.2 versus 67.2) (Figure 1.2H). Combined, this highlights that the model is not sensitive to the experimental design of the training set and predicts broadly across different vector backbones and protein folds.

The ability to predict the experimental data from NYCOMPS allows returning to the question of alkaline phosphatase as a metric for expression. For the training set, proteins with C-termini in the periplasm show weaker fitting by the model (Figure 1.1, orange). To assess the generality of this result, the NYCOMPS outcomes are split into pools for either cytoplasmic or periplasmic C-terminal localization and AUCs are calculated for each. There are no significant differences in predictive capacity across all conditions (Figure 1.2G, green vs. orange) irrespective of whether the tag is at the N- or C-terminus. This demonstrates that the IMProve model is applicable for all topologies.

At this point, it is useful to consider the potential improvement in the number of positive outcomes by using the IMProve model. NYCOMPS tested about a tenth of the 74 thousand possible IMPs from the 98 genomes of interest for expression (Punta et al., 2009). Had NYCOMPS tested the same number of genes from this pool, but selected to have an IMProve score greater than 0.5 (at the 91^st percentile (Figure 1.2C, yellow solid line)), they would have increased their positive pool of 934 by an additional 1207 proteins. This represents a more than two-fold improvement in the return on investment and is a clear benchmark of success for the IMProve model.

1.3.3 Further demonstration of prediction against small-scale independent datasets

The NYCOMPS example demonstrates the predictive power of the model across the broad range of sequence space encompassed by that dataset. Next, the performance of the model is tested against relevant subsets of sequence space (e.g., a family of proteins or the proteome from a single organism), which are reminiscent of laboratory-scale experiments that precede structural or biochemical analyses. While a number of datasets exist (Bernaudat et al., 2011; Eshaghi et al., 2005; Gordon et al., 2008; Korepanova et al., 2005; Lewinson et al., 2008; Lundstrom et al., 2006; Ma et al., 2013; Madhavan et al., 2010; Petrovskaya et al., 2010; Surade et al., 2006; Szakonyi et al., 2007), we identified seven for which complete sequence information could be obtained to calculate all the necessary sequence features (Korepanova et al., 2005; Lundstrom et al., 2006; Ma et al., 2013; Madhavan et al., 2010; Surade et al., 2006).

To understand the predictive performance within each of the small-scale datasets, we analyze the predictive performance of the model and highlight how the model could have been used to streamline those experiments. The clear predictive performance within the large-scale NYCOMPS dataset (Figure 1.2) serves as a benchmark of expected performance at the scale of the experimental efforts for an individual lab (Figure 1.3A). As targets within the various datasets were tested only one or a few times, experimental variability within each set could play a large-role on the outcomes noted. Therefore, we summarize positives within each dataset as those genes with the highest level of outcome as reported by the original authors as this outcome is likely most robust to such variability (e.g., seen via Coomassie Blue staining of an SDS-PAGE gel). To be complete, we have plotted and considered predictive performance across all possible outcomes as well (Figure 1.3B-D, Figure 1.6, Figure 1.7).

Figure 1.3: Success of the model against small scale outcomes. (A) Summary of the model’s performance against NYCOMPS and a variety of small scale expression experiments. Positive outcomes refer to those in the highest group as assigned by the authors of the respective studies. Where targets were tested in more than one condition (e.g., different plasmids or strains), the number of distinct proteins are indicated in parenthesis with a dagger (\(^\dagger\)). (B) The expression of archaeal transporters in up to 6 trials (Ma et al., 2013). Positive expression count is plotted above the dashed line and negative outcomes below the line. (C) Quantitative expression outcomes of those transporters as detected by Coomassie Blue. (D) Receiver Operating Characteristics (ROC) along with Areas Under the Curves (AUC) and 95% confidence interval as well as the total number of positives for the given threshold (red hues) along with the total outcomes (black) are presented. In each curve, increasing expression thresholds are displayed as deeper red.

The performance of the IMProve model for each of the small-scale datasets is consistent with that seen for the NYCOMPS dataset (Figure 1.3A). This is most directly indicated by a mean AUC across all datasets of 65.6, highlighting the success across the varying scales. While the overall positive rate is different for each dataset, considering a cut-off in IMProve score, e.g., the top 50% or 10% of targets ranked by score, would have resulted in a greater percentage of positive outcomes. On average, ~70% of positives are captured within the top half of scores. Similarly, for the top 10% of scores, on average over 20% of the positives are captured. Simply put, for one tenth of the work one would capture a significant number of the positive outcomes within the pool of targets in each dataset.

For broader consideration, one can consider the fold change in positive rate by selecting targets informed by IMProve scores. Using the data available, only testing proteins within the top 10% of scores would result in an average fold change of 2.0 in the positive rate (i.e., twice as many positively expressed proteins). As positive rate is a bounded quantity (maximum is 100%), the possible fold change is bounded as well and becomes relative to the overall positive rate when considering various cut-offs (e.g., for T. maritima the maximum fold-change is 15.4 while for archaeal transporters it is 3.3). Taking the average maximum possible fold change (7.5), the IMProve model achieves nearly a third of the possible improvement in positive rate compared to a perfect predictor.

Since the IMProve model was trained on quantitative expression levels, we also expect that it captures quantitative trends in expression, i.e., a higher score translates to greater amount of expressed protein. While the NYCOMPS results are consistent with this (Figure 1.2b), of the various data sets, only the expression of archaeal transporters presents quantitative outcomes for consideration. For this dataset, 14 archaeal transporters were chosen based on their homology to human proteins (Ma et al., 2013) and tested for expression in E. coli; total protein was quantified in the membrane fraction by Coomassie Blue staining of an SDS-PAGE gel. Here, the majority of the expressing proteins fall into the higher half of the IMProve scores, 7 out of 9 of those with multiple positive outcomes (Figure 1.3B). Strikingly, quantification of the Coomassie Blue staining highlights a clear correlation with the IMProve score where the higher expressing proteins have higher scores (Figure 1.3C).

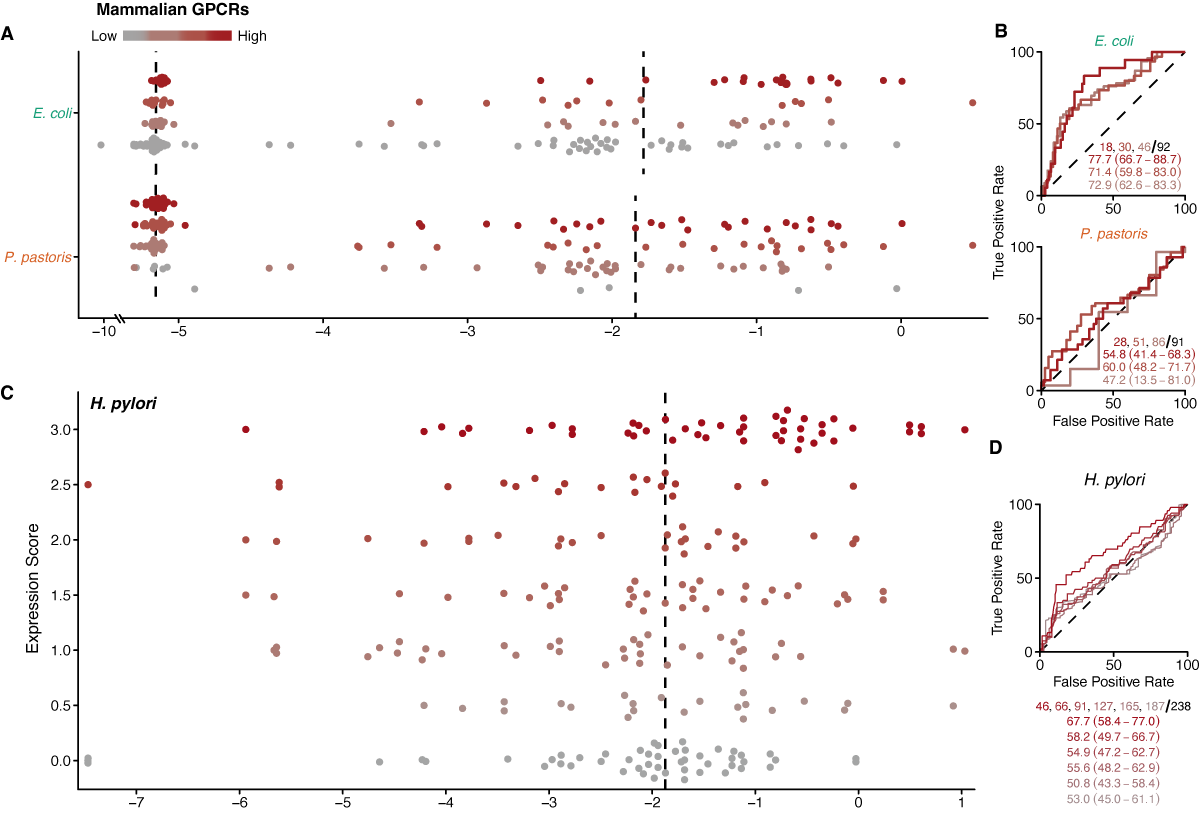
A final test considers the ability of the model to predict expression in hosts other than E. coli. The expression trials of 101 mammalian GPCRs in bacterial and eukaryotic systems (Lundstrom et al., 2006) provides a data set for considering this question. For this experiment, trials in E. coli clearly follow the trend that IMProve can predict within this group of mammalian proteins (AUC = 77.7) (Figure 1.3A, Figure 1.6A,B). However, the expression of the same set of proteins in P. pastoris fails to show any predictive performance (AUC = 54.8) (Figure 1.6A,B). This lack of predictive performance in P. pastoris suggests that the parameterization of the model, calibrated for E. coli expression, requires retraining to generate a different model that captures the distinct interplay of sequence parameters in other hosts.

1.3.4 Biological importance of various sequence features

Considering the success of IMProve, one might anticipate that biological properties driving prediction may provide insight into IMP biogenesis and expression. To derive principles about which features drive prediction, most statistical models (including SVM^rank as used here) require that each data point and its features are drawn identically and distributed independently from an underlying distribution (referred to as “i.i.d.”). In the case of a linear model, if the features meet the i.i.d. criteria then extracting the importance of each feature is straightforward; the weight assigned to each feature corresponds to its relative importance. However, in our case, the input features do not meet the i.i.d. criteria because significant correlation exists between individual features (Figure 1.8).

Since overlapping sets of correlating features represent biological properties, the importance of a given biological property is distributed across many features. The result is that one cannot directly determine the biological underpinnings of the IMProve score. For example, the importance of transmembrane segment hydrophobicity for membrane partitioning is likely distributed between several features: among these the average \(\Delta \text{G}_{\text{insertion}}\) (Hessa et al., 2007) of TM segments has a positive weight whereas average hydrophobicity, a correlating feature, has a negative weight (Table 1.1, Figure 1.8). While this is counterintuitive, it is consistent with the expectation that the overall importance of transmembrane segment hydrophobicity is the sum of many correlated features. While one cannot disentangle the correlation between features, we attempt to address this complication by coarsening our view of the features to two levels: First, we analyze features derived from protein versus those derived from nucleotide sequence, and then we look more closely at features groups after categorizing by biological property.

The coarsest view of the features is a comparison of those derived from protein sequence versus those derived from nucleotide sequence. The summed weight for protein features is around zero, whereas for nucleotide features the summed weight is slightly positive suggesting that in comparison these features may be more important to the predictive performance of the model (Figure 1.4A). Within the training set, protein features more completely explain the score both via correlation coefficients (Figure 1.4B). However, comparison of the predictive performance of the two subsets of weights shows that the nucleotide features alone can give similar performance to the full model for the NYCOMPS dataset (Figure 1.4C). Within the small-scale datasets investigated, using only protein or nucleotide features shows no significant difference in predictive power at 95% confidence (Figure 1.4D). In general, this suggests that neither protein nor nucleotide features are solely responsible for successful IMP expression. However, within the context of the trained model, nucleotide features are critical for predictive performance for a large and diverse dataset such as NYCOMPS. This finding corroborates growing literature that the nucleotide sequence holds significant determinants of biological processes (Chartron et al., 2016; Fluman et al., 2014; Gamble et al., 2016; Goodman et al., 2013; Li et al., 2012).

Figure 1.4: Feature contributions to the model. (A) Classifying features by the type of sequence they are calculated from. (B) Considering the training set (as in Figure 1.1), Spearman correlation coefficients with 95% confidence intervals using individual feature categories for each grouping of data within the training set of E. coli IMPs. Colors indicate the subset being assessed (green, whole cell GFP fluorescence; orange, alkaline phosphatase activity; purple, folded protein by in-gel fluorescence). (C) The AUC and 95% confidence intervals using only protein or nucleotide features. (D) Protein/nucleotide feature dependence across small scale datasets shown as AUCs of the ROC along with 95% CI for the condition with the best overall predictive power (black).

We next collapse conceptually similar features into biological categories that allow us to infer the phenomena that drive prediction. Categories are chosen empirically (e.g., the hydrophobicity group incorporates sequence features such as average hydrophobicity, maximum hydrophobicity, \(\Delta \text{G}_{\text{insertion}}\)), which results in a reduction in overall correlation (Figure 1.9A). The full category list is provided in Table 1.1. To visualize the importance of each category, the collapsed weights are summarized in Figure 1.9B, where each bar contains individual feature weights within a category. Features with a negative weight are stacked to the left of zero and those with a positive weight are stacked to the right. A red dot represents the sum of all weights, and the length of the bar gives the total absolute value of the combined weights within a category. Ranking the categories based on the sum of their weight suggests that some categories play a more prominent role than others. These include properties related to transmembrane segments (hydrophobicity and TM size/count), codon pair score, loop length, and overall length/pI.

To explore the role of each biological category in prediction, the performance of the model is assessed using only features within a given category. First, the strength of the correlation coefficients for given categories within the training set suggests the relative utility of each category for prediction. (Figure 1.9C, as in Figure 1.4B). Examples of categories with high correlation coefficients are 5’ Codon Usage, Length/pI, Loop Length, and SD-like Sites. To verify their importance for prediction, we consider the AUC for prediction using each feature category for the NYCOMPS dataset (Figure 1.9D). In this analysis, only Length/pI shows some predictive power. Overall, the analysis of the training and large-scale testing dataset shows that no feature category independently drives the predictor. Excluding each individually does not significantly affect the overall predictive performance, except for Length/pI (data not shown). Sequence length composes the majority of the weight within this category and is one of the highest weighted features in the model (Figure 1.9A). This is consistent with the anecdotal observation that larger IMPs are typically harder to express. However, this parameter alone would not be useful for predicting within a smaller subset, like a single protein family, where there is little variance in length (e.g., Figure 1.3,Figure 1.5). One might develop a predictor that was better for a given protein family under certain conditions with a subset of the entire features considered here; yet this would require a priori knowledge of the system, i.e., which sequence features were truly most important, and would preclude broad generalizability as shown for the IMProve model.

1.3.5 Usage of the IMProve model for IMP expression

We illustrate the IMProve model’s ability to identify promising homologs within a protein family by considering subsets of the broad range of targets tested by NYCOMPS. First, we consider two examples for protein families that do not have associated atomic resolution structures: copper resistance proteins (CopD, PF05425) and short-chain fatty-acid transporters (AtoE, PF02667). In the first two rows of Figure 1.5A, genes from the two families are plotted by IMProve score and colored by experimental outcome. In both cases, as indicated by the AUCs of 88.2 and 80.7 (Figure 1.5A), the model excels at predicting these families and provides a clear score cut-off to guide target selection for future expression experiments. For example, we expect that CopD homologs with IMProve scores above -1 will have a higher likelihood of expressing over other homologs.

Figure 1.5: Usage of the model within IMP families and for optimization of expression level. (A) Outcomes for specific protein families with an optimal IMProve score threshold indicated. Genes are shown in the chart as dots colored based on outcomes from trials: Only Positive (red), Only Negative (grey), and Mixed (blue). Overall statistics, as in Table 1.3, are noted. Dashed lines represent the optimal threshold from the ROC curves. For the top two rows, each was only tested in a single condition (N: His-FLAG-TEV-gene). The bottom three rows are larger pools from NYCOMPS where there are multiple trials for many of the genes. (B) A table curated from Table 1.3 where Pfams were selected based on specific criteria (minimum 10 trials, 4 positive and 4 negative outcomes) and ordered by AUC. Proteins, as in A, that have known crystal structures within the family are highlighted in purple. DUFs are domains of unknown function. For context, the following Pfam families correspond to TCDB classes: PF05425, 9.B.62; PF02667, 2.A.73; PF03595, 2.A.16; PF00999, 2.A.36, 2.A.37; PF00535, 9.B.32; PF03601, 2.A.98; PF02537, 1.A.43; PF01757, 9.B.97; PF02378, 4.A.1, 4.A.2, 4.A.3; PF02690, 2.A.58; PF02632, 2.A.88 (Saier et al., 2016). (C) A comparison of the predictive capacity of IMProve compared to using silent mutations engineered to increase anti-SD sequence binding propensity (Fluman et al., 2014). The table presents experimental relative expression level (mutant over wild-type sequence) versus predictions from relative changes in either IMProve score or SD-like sites. The cells are colored as a heat map from red (lower than wildtype) to blue (higher than wildtype).

We have calculated predictive performance for each Pfam found in the NYCOMPS data which allows us to provide considerations for future experiments (Table 1.3). In particular, we highlight three families with many genes tested, multiple experimental trials and a spread of outcomes: voltage-dependent anion channels (PF03595), Na/H exchangers (PF00999), and glycosyltransferases (PF00535). For these, a very clear IMProve score cut-off emerges from the experimental outcomes (dashed line in Figure 1.5A). Strikingly, for these families the IMProve model clearly ranks the targets with Only Positive outcomes (red) at higher scores, again suggesting a preference for the best expressing proteins (see Figure 1.2 and Figure 1.3). Similarly, many more families within NYCOMPS are predicted with high statistical confidence (Table 1.3); we provide a subset as Figure 1.5B. For these, if only genes in the top 50% of IMProve score were tested, 81% of the total positives would be captured. As noted before, this is a dramatic increase in efficiency. Excitingly, many of these families remain to be resolved structurally. Considering these results with the broader experimental data sets (Figure 1.3), no matter the number of proteins one is willing to test, the IMProve model enables selecting targets with a high probability of expression success in E. coli.

1.3.6 Sequence optimization for expression

The predictive performance of the model implies that the features defined here provide a coarse approximation of the fitness landscape for IMP expression. Attempting to optimize a single feature by modifying the sequence will likely affect the resulting score and expression due to changes in other features. Fluman, et al. provides an illustrative experiment (Fluman et al., 2014). For that work, it was hypothesized that altering the number of Shine-Dalgarno (SD)-like sites in the coding sequence of a IMP would affect expression level. To test this, silent mutations were engineered within the first 200 bases of three proteins (genes ygdD, brnQ, and ybjJ from E. coli) to increase the number of SD-like sites with the goal of improving expression. Expression trials demonstrated that only one of the proteins (BrnQ) had improved expression of folded protein. While the number of SD-like sites alone does not correlate, only 1 out of 3, the resulting changes in the IMProve score correlate with the changes in measured expression level, 3 out of 3 (Figure 1.5C). The IMProve model’s ability to capture the outcomes in this small test case illustrates the utility of integrating the contribution of the numerous parameters involved in IMP biogenesis.

1.4 Discussion

Here, we have demonstrated a statistically driven predictor, IMProve, that decodes from sequence the sum of biological features that drive expression, a feat not previously possible (Nørholm et al., 2013). The current best practice for characterization of an IMP target begins with the identification and testing of multiple homologs or variants for expression. The predictive power of IMProve enables this by providing a low barrier-to-entry method to enrich for positive outcomes by more than two-fold. IMProve allows for the prioritization of targets to test for expression making more optimal use of limited human and material resources. For groups with small scale projects such as individual labs, this means that for the same cost one would double the success rate. For large scale groups, such as companies or consortia, IMProve can reduce by half the cost required to obtain the same number of positive results. We provide the current predictor as a web service where scores can be calculated, and the method, associated data, and suggested analyses are publically available to catalyze progress across the community (clemonslab.caltech.edu).

Having shown that IMP expression can be predicted, the generalizability of the model is remarkable despite several known limitations that will be investigated in next generation predictors. Using data from a single study for training precluded including certain features that empirically influence expression level such as fusion tags and the context of the protein in an expression plasmid, e.g., the 5’ untranslated region, for which there was no variation in the Daley, Rapp, et al. dataset. Moreover, using a simple proof-of-concept linear model allowed for a straightforward and robust predictor; however, intrinsically it cannot be directly related to the biological underpinnings. While we can extract some biological inference, a linear combination of sequence features does not explicitly reflect the reality of physical limits for host cells. To some extent, constraint information is likely encoded in the complex architecture of the underlying sequence space (e.g., through the genetic code, TM prediction, RNA secondary structure analyses). Future statistical models that improve on these limitations will hone predictive power and more intricately characterize the interplay of variables that underlie IMP expression. By building upon the methodology here and by careful analysis of datasets in the literature, we expect to train IMP expression predictors for other host systems (e.g., eukaryotic cells).

A surprising outcome of our results is the observation of a quantitatively important contribution of the nucleotide sequence as a component of the IMProve score. This echoes the growing literature that aspects of the nucleotide sequence are important determinants of protein biogenesis in general (Chartron et al., 2016; Fluman et al., 2014; Gamble et al., 2016; Goodman et al., 2013; Li et al., 2012). While one expects that there may be different weights for various nucleotide derived features between soluble and IMPs, it is likely that these features are important for soluble proteins as well. An example of this is the importance of codon optimization for soluble protein expression, which has failed to show any general benefit for IMPs (Nørholm et al., 2012). Current expression predictors that have predictive power for soluble proteins have only used protein sequence for deriving the underlying feature set (Slabinski et al., 2007b; Wang et al., 2016). Future prediction methods will likely benefit from including nucleotide sequence features as done here.

The ability to predict phenotypic results using sequence based statistical models opens a variety of opportunities. As done here, this requires a careful understanding of the system and its underlying biological processes enumerated in a multitude of individual variables that impact the stated goal of the predictor, in this case enriching protein expression. As new features related to expression are discovered, future work will incorporate these leading to improved models. This can include features derived from other approaches such as the integration efficiency from coarse-grained molecular dynamics (Marshall et al., 2016; Niesen et al., 2017) and 5’ mRNA secondary structure/translation initiation efficiency (Goodman et al., 2013; Mirzadeh et al., 2015; Reis and Salis, 2020). Based on these results, expanding to new expression hosts such as eukaryotes seems entirely feasible, although a number of new features may need to be considered, e.g., glycosylation sites and trafficking signals. Moreover, the ability to score proteins for expressibility creates new avenues to computationally engineer IMPs for expression. The proof-of-concept described here required significant work to compile data from genomics consortia and the literature in a readily useable form. As data becomes more easily accessible, broadly leveraging diverse experimental outcomes to decode sequence-level information, an extension of this work, is anticipated.

1.5 Materials and Methods

Sequence mapping & retrieval and feature calculation was performed in Python 2.7 (Van Rossum and Drake Jr, 1995) using BioPython (Cock et al., 2009) and NumPy (van der Walt et al., 2011); executed and consolidated using Bash (shell) scripts; and parallelized where possible using GNU Parallel (Tange, 2011). Data analysis and presentation was done in R (R Core Team, 2015) within RStudio (RStudio Team, 2015) using magrittr (Bache and Wickham, 2014), plyr (Wickham, 2011), dplyr (Wickham and Francois, 2015), asbio (Aho, 2015), and datamart (Weinert, 2014) for data handling; ggplot2 (Wickham, 2016, p. 2), ggbeeswarm (Clarke and Sherrill-Mix, 2015), GGally (Schloerke et al., 2016), gridExtra (Auguie, 2015), cowplot (Wilke, 2015), scales (Wickham, 2015), viridis (Garnier, 2016), and RColorBrewer (Harrower and Brewer, 2003; Neuwirth, 2014) for plotting; multidplyr (Wickham, n.d.) with parallel (R Core Team, 2015) and foreach (Revolution Analytics and Weston, 2015a) with iterators (Revolution Analytics and Weston, 2015b) and doMC (Revolution Analytics and Weston, 2015c)/doParallel (Revolution Analytics and Weston, 2015d) for parallel processing; and roxygen2 (Wickham et al., 2015) for code organization and documentation as well as other packages as referenced.

1.5.1 Collection of data necessary for learning and evaluation

E. coli Sequence Data

The nucleotide sequences from (Daley et al., 2005) were deduced by reconstructing forward and reverse primers (i.e., ~20 nucleotide stretches) from each gene in Colibri (based on EcoGene 11), the original source cited and later verified these primers against an archival spreadsheet provided directly by Daniel Daley (personal communication). To account for sequence and annotation corrections made to the genome after Daley, Rapp, et al.’s work, these primers were directly used to reconstruct the amplified product from the most recent release of the E. coli K-12 substr. MG1655 genome (Zhou and Rudd, 2013) (EcoGene 3.0; U00096.3). Although Daniel Daley mentioned that raw reads from the Sanger sequencing runs may be available within his own archives, it was decided that the additional labor to retrieve this data and parse these reads would not significantly impact the model. The deduced nucleotide sequences were verified against the protein lengths given in Supplementary Table 1 from (Daley et al., 2005). The plasmid library tested in (Fluman et al., 2014) was provided by Daniel Daley, and those sequences are taken to be the same.

E. coli Training Data

The preliminary results using the mean-normalized activities echoed the findings of (Daley et al., 2005) that these do not correlate with sequence features either in the univariate sense (many simple linear regressions, Supplementary Table 1 (Daley et al., 2005)) or a multivariate sense (multiple linear regression, data not shown). This is presumably due to the loss of information regarding variability in expression level for given genes or due to the increase in variance of the normalized quantity (See Section 1.5.4) due to the normalization and averaging procedure. Daniel Daley and Mikaela Rapp provided spreadsheets of the outcomes from the 96-well plates used for their expression trials and sent scanned copies of the readouts from archival laboratory notebooks where the digital data was no longer accessible (personal communication). Those proteins without a reliable C-terminal localization (as given in the original work) or without raw expression outcomes were not included in further analyses.

Similarly, Nir Fluman also provided spreadsheets of the raw data from the set of three expression trials performed in (Fluman et al., 2014).

New York Consortium on Membrane Protein Structure (NYCOMPS) Data

Brian Kloss, Marco Punta, and Edda Kloppman provided a dataset of actions performed by the NYCOMPS center including expression outcomes in various conditions (Love et al., 2010; Punta et al., 2009). The protein sequences were mapped to NCBI GenInfo Identifier (GI) numbers either via the Entrez system (Schuler et al., 1996) or the Uniprot mapping service (UniProt Consortium, 2012). Each GI number was mapped to its nucleotide sequence via a combination of the NCBI Elink mapping service and the “coded_by” or “locus” tags of Coding Sequence (CDS) features within GenBank entries. Though custom-purpose code was written, a script from Peter Cock is available to do the same task via a similar mapping mechanism (Cock, 2009). To confirm all sequences, the TargetTrack (Chen et al., 2004) XML file was parsed for the internal NYCOMPS identifiers and compared for sequence identity to those that had been mapped using the custom script; 20 (less than 1%) of the sequences had minor inconsistencies and were manually replaced.

Archaeal transporters Data

The locus tags (“Gene Name” in Table 1) were mapped directly to the sequences and retrieved from NCBI (Ma et al., 2013). Pikyee Ma and Margarida Archer clarified questions regarding their work to inform the analysis.

GPCR Expression Data

Nucleotide sequences were collected by mapping the protein identifiers given in Table 1 from (Lundstrom et al., 2006) to protein GIs via the Uniprot mapping service (UniProt Consortium, 2012) and subsequently to their nucleotide sequences via the custom mapping script described above (see NYCOMPS 1.5.1.3). The sequence length and pI were validated against those provided. Renaud Wagner assisted in providing the nucleotide sequences for genes whose listed identifiers were unable to be mapped and/or did not pass the validation criteria as the MeProtDB (the sponsor of the GPCR project) does not provide a public archive.

Helicobacter pylori Data

Nucleotide sequences were retrieved by mapping the locus tags given in Supplemental Table 1 from (Psakis et al., 2007) to locus tags in the Jan 31, 2014 release of the H. pylori 26695 genome (AE000511.1). To verify sequence accuracy, sequences whose molecular weight matched that given by the authors were accepted. Those that did not match, in addition to the one locus tag that could not be mapped to the Jan 31, 2014 genome version, were retrieved from the Apr 9, 2015 release of the genome (NC_000915.1). Both releases are derived from the original sequencing project (Tomb et al., 1997). After this curation, all mapped sequences matched the reported molecular weight.

In this data set, expression tests were performed in three expression vectors and scored as 1, 2, or 3. Two vectors were scored via two methods. For these two vectors, the two scores were averaged to give a single number for the condition making them comparable to the third vector while yielding 2 additional thresholds (1.5 and 2.5) result in the 5 total curves shown (Figure 1.8B).

Mycobacterium tuberculosis Data

The authors note using TubercuList through GenoList (Lechat et al., 2008), therefore, nucleotide sequences were retrieved from the archival website based on the original sequencing project (Cole et al., 1998). The sequences corresponding to the identifiers and outcomes in Table 1 from (Korepanova et al., 2005) were validated against the provided molecular weight .

Secondary Transporter Data

GI Numbers given in Table 1 from (Surade et al., 2006) were matched to their CDS entries using the custom mapping script described above (see NYCOMPS 1.5.1.3). Only expression in E. coli with IPTG-inducible vectors was considered.

Thermotoga maratima Data

Gene names given in Table 1 (Dobrovetsky et al., 2005) were matched to CDS entries in the Jan 31, 2014 release of the Thermotoga maritima MSB8 genome (AE000512.1), a revised annotation of the original release (Nelson et al., 1999). The sequence length and molecular weight were validated against those provided.

Pseudomonas aeruginosa Data

Outcomes in Additional file 1 (Madhavan et al., 2010) were matched to coding sequences provided by Constance Jeffrey.

Shine-Dalgarno-like mutagenesis Data

Folded protein is quantified by densitometry measurement (Schindelin et al., 2012; Schneider et al., 2012) of the relevant band in Figure 6 of (Fluman et al., 2014). Relative difference is calculated as is standard (Equation 1.2):

\[ \frac{\text{metric}_\text{mutant} - \text{metric}_\text{wildtype}}{\frac{1}{2}\left| \text{metric}_\text{mutant} - \text{metric}_\text{wildtype} \right|} \tag{1.2}\]

1.5.2 Details related to the calculation of sequence features

Transmembrane segment topology was predicted using Phobius Constrained for the training data and Phobius for all other datasets (Käll et al., 2004). We were able to obtain the Phobius code and integrate it directly into our feature calculation pipeline resulting in significantly faster speeds than any other option. Several features were obtained by averaging per-site metrics (e.g., per-residue RONN3.2 disorder predictions) in windows of a specified length. Windowed tAI metrics are calculated over all 30 base windows (not solely over 10 codon windows). Table 1.1 includes an in-depth description of each feature. Future work will explore contributions of elements outside the gene of interest, e.g., ribosomal binding site, linkers, tags.

1.5.3 Preparation for model learning

Calculated sequence features for the IMPs in the E. coli dataset as well as raw activity measurements, i.e., each 96-well plate, were loaded into R. As is best practice in using Support Vector Machines, each feature was “centered” and “scaled” where the mean value of a given feature was subtracted from each data point and then divided by the standard deviation of that feature using preprocess (Kuhn, 2008). As is standard practice, the resulting set was then culled for those features of near zero-variance, over 95% correlation (Pearson’s r), and linear dependence (nearZeroVar, findCorrelation, findLinearCombos)(Kuhn, 2008). In particular this procedure removed extraneous degrees of freedom during the training process which carry little to no additional information with respect to the feature space and which may over represent certain redundant features. Features and outcomes for each list (“query”) were written into the SVM^light format using a modified svmlight.write (Weihs et al., 2005).

The final features were calculated for each sequence in the test datasets, prepared for scoring by “centering” and “scaling” by the training set parameters via preprocess (Kuhn, 2008), and then written into SVM^light format again using a modified svmlight.write.

1.5.4 Model selection, training, and evaluation using SVM^rank

At the most basic level, our predictive model is a learned function that maps the parameter space (consisting of nucleotide and protein sequence features) to a response variable (expression level) through a set of governing weights (\(\vec{w}_1, \vec{w}_2, \ldots , \vec{w}_N\)). Depending on how the response variable is defined, these weights can be approximated using several different methods. As such, defining a response variable that is reflective of the available training data is key to selecting an appropriate learning algorithm.

The quantitative 96-well plate results (Daley et al., 2005) that comprise our training data do not offer an absolute expression metric valid over all plates—the top expressing proteins in one plate would not necessarily be the best expressing within another. As such, this problem is suited for preference-ranking methods. As a ranking problem, the response variable is the ordinal rank for each protein derived from its overexpression relative to the other members of the same plate of expression trials. In other words, the aim is to rank highly expressed proteins (based on numerous trials) at higher scores than lower expressed proteins by fitting against the order of expression outcomes from each constituent 96-well plate.

As the first work of this kind, the aim was to employ the simplest framework necessary taking in account the considerations above. The method chosen computes all valid pairwise classifications (i.e., within a single plate) transforming the original ranking problem into a binary classification problem. The algorithm outputs a score for each input by minimizing the number of swapped pairs thereby maximizing Kendall’s \(\tau\) (Kendall, 1938). For example, consider the following data generated via context \(A\): \((X_{A,1},\ Y_{A,1}), (X_{A,2},Y_{A,2})\) and \(B\): \((X_{B,1}, Y_{B,1}), (X_{B,2},Y_{B,2})\) where observed response follows as index \(i\), i.e., \(Y_{n} < Y_{n + 1}\). Binary classifier f (\(X_{i},\ X_{j})\) gives a score of 1 if an input pair matches its ordering criteria and \(- 1\) if not, i.e., \(Y_{i} < Y_{j}\):

\[ f\left( X_{A,1},X_{A,2} \right) = 1;f\left( X_{A,2},X_{A,1} \right) = - 1 \]

\[ f\left( X_{B,1},X_{B,2} \right) = 1;f\left( X_{B,2},X_{B,1} \right) = - 1 \]

\[ f\left( X_{A,1},X_{B,2} \right), f\left( X_{A,2},X_{B,1} \right) \text{ are invalid} \]

Free parameters describing \(f\) are calculated such that those calculated orderings \(f\left( X_{A,1} \right),f\left( X_{A,2} \right)\ldots;\ f\left( X_{B,1} \right),f\left( X_{B,2} \right)\ldots\) most closely agree (overall Kendall’s \(\tau\)) with the observed ordering \(\ Y_{n},\ Y_{n + 1},\ \ldots\). In this sense, \(f\) is a pairwise Learning to Rank method.

Within this class of models, a linear preference-ranking Support Vector Machine was employed (Joachims, 2002). To be clear, as an algorithm a preference-ranking SVM operates similarly to the canonical SVM binary classifier. In the traditional binary classification problem, a linear SVM seeks the maximally separating hyper-plane in the feature space between two classes, where class membership is determined by which side of the hyper-plane points reside. For some \(n\) linear separable training examples \(D = {\left\{ \ \left( x_{i} \right) \right|\ x_{i}\ \epsilon\ \mathbb{R}^{d}\}}^{n}\) and two classes \(y_{i}\ \epsilon\ \{ - 1,\ 1\}\), a linear SVM seeks a mapping from the d-dimensional feature space \(\mathbb{R}^{d} \rightarrow \{ - 1,\ 1\}\) by finding two maximally separated hyperplanes \(w\ \bullet x\ - b = 1\) and \(\ w\ \bullet x\ - b = - \ 1\) with constraints that \(w\ \bullet x_{i}\ - b \geq 1\ \)for all \(x_{i}\) with \(y_{i}\ \epsilon\ \{ 1\}\) and \(w\ \bullet x_{i}\ - b \leq \ - \ 1\) for all \(x_{i}\) with \(y_{i}\ \epsilon\ \{ - 1\}\). The feature weights correspond to the vector \(\vec{w}\), which is the vector perpendicular to the separating hyperplanes, and are computable in \(O(n\log{}n)\) implemented as part of the SVM^rank^ software package, though in \(O(n^2)\) (Tsochantaridis et al., 2005). See (Joachims, 2002) for an in-depth, technical discussion.

In a soft-margin SVM where training data is not linearly separable, a tradeoff between misclassified inputs and separation from the hyperplane must be specified. This parameter \(C\) was found by training models against raw data from Daley, Rapp, et al. with a grid of candidate \(C\) values (\(2^{n}\ \forall\ n\ \epsilon\ \lbrack - 5,\ \ 5\rbrack\)) and then evaluated against the raw “folded protein” measurements from Fluman, et al. The final model was chosen by selecting that with the lowest error from the process above (\(C = 2^5\)). To be clear, the final model is composed solely of a single weight for each feature; the tradeoff parameter \(C\) is only part of the training process.

Qualitatively, such a preference-ranking method constructs a model that ranks groups of proteins with higher expression level higher than other groups with lower expression value. In comparison to methods such as linear regression and binary classification, this approach is more robust and less affected by the inherent stochasticity of the training data.

1.5.5 Quantitative Assessment of Predictive Performance

In generating a predictive model, one aims to enrich for positive outcomes while ensuring they do not come at the cost of increased false positive diagnoses. This is formalized in Receiver Operating Characteristic (ROC) theory (for a primer see (Swets et al., 2000)), where the true positive rate is plotted against the false positive rate for all classification thresholds (score cutoffs in the ranked list). In this framework, the overall ability of the model to resolve positive from negative outcomes is evaluated by analyzing the Area Under a ROC curve (AUC) where AUC_perfect=100% and AUC_random=50% (percentage signs are omitted throughout the text and figures). All ROCs are calculated through pROC (Robin et al., 2011) using the analytic Delong method for AUC confidence intervals (DeLong et al., 1988). Bootstrapped AUC CIs (\(N = 10^6\)) were precise to 4 decimal places suggesting that analytic CIs are valid for the NYCOMPS dataset.

With several of our datasets, no definitive standard or clear-cut classification for positive expression exists. However, the aim is to show and test all reasonable classification thresholds of positive expression for each dataset in order to evaluate predictive performance as follows:

Training data

The outcomes are quantitative (activity level), so each ROC is calculated by normalizing within each dataset to the standard well subject to the discussion in 4a above (LepB for PhoA, and InvLepB for GFP) (examples in Figure 1.1D) for each possible threshold, i.e., each normalized expression value with each AUC plotted in Figure 1.1E. 95% confidence intervals of Spearman’s \(\rho\) are given by 10⁶ iterations of a bias-corrected and accelerated (BCa) bootstrap of the data (Figure 1.1A,C) (Canty and Ripley, 2015).

Large-scale

ROCs were calculated for each of the expression classes (Figure 1.2E). Regardless of the split, predictive performance is noted. The binwidth for the histogram was determined using the Freedman-Diaconis rule(Freedman and Diaconis, 1981), and scores outside the plotted range comprising <0.6% of the density were implicitly hidden.

Small-scale

Classes can be defined in many different ways. To be principled about the matter, ROCs for each possible cutoff are presented based on definitions from each publication (Figure 1.3C,E,G; Figure 1.8B,D,F). See Section 1.5.1 for any necessary details about outcome classifications for each dataset.

1.5.6 Feature Weights

Weights for the learned SVM are pulled directly from the model file produced by SVM^light and are given in Table 1.1.

1.5.7 Availability

All analysis is documented in a series of R notebooks (Xie, 2014) available openly at github.com/clemlab/ml-ecoli-IMProve. These notebooks provide fully executable instructions for the reproduction of the analyses and the generation of figures and statistics in this study. The IMProve model is available as a web service at clemonslab.caltech.edu.

1.6 Acknowledgements

We thank Daniel Daley and Thomas Miller’s group for discussion, Yaser Abu-Mostafa and Yisong Yue for guidance regarding machine learning, Niles Pierce for providing NUPACK source code (Zadeh et al., 2011), Welison Floriano and Naveed Near-Ansari for maintaining local computing resources, and Samuel Schulte for suggesting the model’s name. We thank Michiel Niesen, Stephen Marshall, Thomas Miller, Reid van Lehn, James Bowie, and Tom Rapoport for comments on the manuscript. Models and analyses are possible thanks to raw experimental data provided by Daniel Daley and Mikaela Rapp (Daley et al., 2005); Nir Fluman (Fluman et al., 2014); Edda Kloppmann, Brian Kloss, and Marco Punta from NYCOMPS (Love et al., 2010; Punta et al., 2009); Pikyee Ma (Ma et al., 2013); Renaud Wagner (Lundstrom et al., 2006); Florent Bernaudat (Bernaudat et al., 2011), and Constance Jeffrey (Madhavan et al., 2010).

We acknowledge funding from an NIH Pioneer Award to WMC (5DP1GM105385); a Benjamin M. Rosen graduate fellowship, a NIH/NRSA training grant (5T32GM07616), and a NSF Graduate Research fellowship to SMS; and an Arthur A. Noyes Summer Undergraduate Research Fellowship to NJ. Computational time was provided by Stephen Mayo and Douglas Rees. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1144469. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575 (Towns et al., 2014).

1.7 Supplementary Figures

Figure 1.6: Success of the model against a variety of small scale outcomes. For each set, vertical lines indicate the median IMProve score. Receiver Operating Characteristics (ROC) along with Areas Under the Curves (AUC) and 95% confidence interval as well as the total number of positives for the given threshold (red hues) along with the total outcomes (black) are presented. In each curve, increasing expression thresholds as defined by the original publication are displayed as deeper red. The Receiver Operating Characteristic (ROC) with each cutoff is plotted, where a higher cutoff is represented by a deeper red, followed by the Area Under the Curves (directly below) in colors that correspond to the respective curve. (A,B) Mammalian GPCR expression in either E. coli (top, green) or P. pastoris (bottom, orange). (C,D) Experimental expression of 116 H. pylori membrane proteins in E. coli in at most 3 vectors (238 trials) scored as either a 1, 2, or 3 from the outcome of a dot blot as well as Coomassie Staining of an SDS-PAGE gel for two of the vectors. To compare the three vectors with a single set of scores, the two scores were averaged to give a single number for a condition making them comparable to the third vector while yielding 2 additional thresholds (1.5 and 2.5) and the 6 total levels shown.

Figure 1.7: Success of the model against a variety of small scale outcomes. For each set, vertical lines indicate the median IMProve score. Receiver Operating Characteristics (ROC) along with Areas Under the Curves (AUC) and 95% confidence interval as well as the total number of positives for the given threshold (red hues) along with the total outcomes (black) are presented. In each curve, increasing expression thresholds as defined by the original publication are displayed as deeper red. The Receiver Operating Characteristic (ROC) with each cutoff is plotted, where a higher cutoff is represented by a deeper red, followed by the Area Under the Curves (directly below) in colors that correspond to the respective curve. (E,F) Experimental expression of M. tuberculosis membrane proteins plotted based on outcomes. (G,H) Pooled outcomes from the expression of 87 P. aeruginosa membrane proteins in E. coli across 3 plasmids and 2 strains scored on a relative scale. (I,J) Expression of 77 T. maritima membrane proteins in E. coli noted as purified (5), not purified but expressed (14), or neither. (K,L) Expression of 37 microbial secondary transporters in 4 IPTG-inducible vectors (144 trials) in E. coli quantified as 10 ng/mL (pink) or 100 ng/mL (red) via dot blot.

Figure 1.8: Complete set of feature correlations and their individual contributions to the model. Features are ordered first by category and then by weight (grey bars). Labels are green for protein-sequence derived and brown for nucleotide-sequence derived features. Pearson correlation coefficient between each pair of features across the NYCOMPS dataset is plotted (right). See Table 1.1 for a detailed description of each feature. Feature categories are overlaid as square boxes and indicated by black bars on the top, left, and right of the correlation matrix.

Figure 1.9: Feature contributions to the model across datasets used for training and validation. (A) Pearson correlation coefficients between feature categories are shown. Feature labels are green for protein-sequence derived and brown for nucleotide-sequence derived. (B) Total weight for each category is represented as a bar. The contribution of each feature to the category is shown by partitioning the bar. The red dot indicat es the total sum of weights within the category. (C) Feature category dependence within the training set is shown by Spearman’s \(\rho\) and 95% CI between the normalized outcomes versus the feature subset. (D) Considering the NYCOMPS data set (as in Figure 1.2), the Area Under the Curve (AUC) of a Receiver Operating Characteristic and 95% confidence interval when predicting solely by features from the specified category against the NYCOMPS dataset. Red, using positive only as the cut-off for individual genes (Figure 1.2C); grey, using positive outcomes within each plasmid and solubilization condition (as in Figure 1.2E).

1.8 Supplementary Tables

Table 1.1: Sequence parameter weights and descriptions. Weights are presented after normalizing to the mean value for clarity. Features that were calculated but removed in pre-processing are noted (Section 1.5.3).

Table 1.2: AUC values for the NYCOMPS dataset. AUC values and 95% confidence intervals are presented in summary, by expression condition, and by predicted C-terminal localization as well as for IMProve scores calculated without the most computationally expensive RNA secondary structure calculation.

Pfam ID	Pfam Name	Expression Trials	Positive Outcomes	Negative Outcomes	AUC (95% CI)
PF00359.19	PTS_EIIA_2	14	3	11	1.00 (1.00-1.00)
PF02656.12	DUF202	10	9	1	1.00 (1.00-1.00)
PF03186.10	CobD_Cbib	11	1	10	1.00 (1.00-1.00)
PF03176.12	MMPL	105	1	104	0.99 (0.99-0.99)
PF02683.12	DsbD	18	1	17	0.97 (0.97-0.97)
PF02355.13	SecD_SecF	33	1	32	0.97 (0.97-0.97)
PF12822.4	DUF3816	11	4	7	0.96 (0.87-1.00)
PF00662.17	Proton_antipo_N	120	2	118	0.94 (0.87-1.00)
PF04247.9	SirB	16	1	15	0.93 (0.93-0.93)
PF06127.8	DUF962	11	6	5	0.93 (0.78-1.00)
PF11742.5	DUF3302	15	1	14	0.93 (0.93-0.93)
PF01610.14	DDE_Tnp_ISL3	14	2	12	0.92 (0.73-1.00)
PF07290.8	DUF1449	11	1	10	0.90 (0.90-0.90)
PF02659.12	Mntp	29	2	27	0.89 (0.76-1.00)
PF04217.10	DUF412	12	5	7	0.89 (0.65-1.00)
PF05425.10	CopD	20	3	17	0.88 (0.73-1.00)
PF02535.19	Zip	34	1	33	0.86 (0.86-0.86)
PF02667.11	SCFA_trans	19	7	12	0.86 (0.68-1.00)
PF01810.15	LysE	41	2	39	0.83 (0.59-1.00)
PF06930.9	DUF1282	12	5	7	0.83 (0.57-1.00)
PF03595.14	SLAC1	76	19	57	0.81 (0.67-0.94)
PF04172.13	LrgB	63	4	59	0.79 (0.57-1.00)
PF03601.11	Cons_hypoth698	52	9	43	0.78 (0.64-0.92)
PF02537.12	CRCB	81	20	61	0.77 (0.66-0.88)
PF01757.19	Acyl_transf_3	23	6	17	0.76 (0.53-1.00)
PF02378.15	PTS_EIIC	82	15	67	0.76 (0.62-0.90)
PF03929.13	PepSY_TM	25	2	23	0.76 (0.36-1.00)
PF00999.18	Na_H_Exchanger	398	21	377	0.76 (0.66-0.86)
PF00535.23	Glycos_transf_2	282	62	220	0.76 (0.70-0.82)
PF03605.11	DcuA_DcuB	28	2	26	0.75 (0.32-1.00)
PF02690.12	Na_Pi_cotrans	64	9	55	0.75 (0.54-0.95)
PF01699.21	Na_Ca_ex	75	4	71	0.74 (0.58-0.90)
PF03390.12	2HCT	18	3	15	0.73 (0.37-1.00)
PF00950.14	ABC-3	33	7	26	0.73 (0.51-0.94)
PF06762.11	LMF1	17	1	16	0.72 (0.72-0.72)
PF03741.13	TerC	19	4	15	0.72 (0.42-1.00)
PF02632.11	BioY	47	15	32	0.71 (0.54-0.88)
PF06738.9	ThrE	26	2	24	0.71 (0.42-1.00)
PF11911.5	DUF3429	36	12	24	0.70 (0.53-0.88)
PF01226.14	Form_Nir_trans	13	8	5	0.70 (0.38-1.00)
PF09586.7	YfhO	6	1	5	0.70 (0.70-0.70)
PF03739.11	YjgP_YjgQ	214	17	197	0.70 (0.56-0.84)
PF05656.11	DUF805	100	21	79	0.69 (0.56-0.81)
PF01566.15	Nramp	129	21	108	0.69 (0.55-0.82)
PF05977.10	MFS_3	12	3	9	0.69 (0.37-1.00)
PF03023.11	MVIN	67	7	60	0.68 (0.46-0.90)
PF02674.13	Colicin_V	32	4	28	0.68 (0.47-0.89)
PF03009.14	GDPD	46	1	45	0.68 (0.68-0.68)
PF10110.6	GPDPase_memb	46	1	45	0.68 (0.68-0.68)
PF01545.18	Cation_efflux	21	5	16	0.68 (0.32-1.00)
PF07854.9	DUF1646	7	1	6	0.67 (0.67-0.67)
PF01594.13	UPF0118	436	137	299	0.67 (0.61-0.72)
PF06541.8	ABC_trans_CmpB	33	2	31	0.66 (0.51-0.81)
PF12698.4	ABC2_membrane_3	248	13	235	0.65 (0.46-0.85)
PF01578.17	Cytochrom_C_asm	53	5	48	0.65 (0.39-0.92)
PF00520.28	Ion_trans	17	4	13	0.65 (0.35-0.95)
PF00230.17	MIP	83	35	48	0.65 (0.53-0.77)
PF04608.10	PgpA	31	11	20	0.65 (0.43-0.87)
PF03062.16	MBOAT	78	5	73	0.65 (0.36-0.94)
PF01569.18	PAP2	8	1	7	0.64 (0.64-0.64)
PF03788.11	LrgA	55	3	52	0.64 (0.36-0.92)
PF03824.13	NicO	15	3	12	0.64 (0.26-1.00)
PF03222.10	Trp_Tyr_perm	13	5	8	0.64 (0.35-0.92)
PF01040.15	UbiA	212	29	183	0.63 (0.53-0.73)
PF02517.13	Abi	47	13	34	0.63 (0.43-0.82)
PF07690.13	MFS_1	378	45	333	0.62 (0.54-0.71)
PF00854.18	PTR2	103	17	86	0.62 (0.49-0.76)
PF01627.20	Hpt	14	3	11	0.62 (0.30-0.94)
PF00361.17	Proton_antipo_M	648	19	629	0.62 (0.51-0.72)
PF02592.12	Vut_1	34	7	27	0.61 (0.39-0.84)
PF01758.13	SBF	126	22	104	0.61 (0.48-0.74)
PF00860.17	Xan_ur_permease	559	115	444	0.61 (0.55-0.67)
PF02702.14	KdpD	24	3	21	0.61 (0.22-1.00)
PF13231.3	PMT_2	111	8	103	0.61 (0.43-0.78)
PF00474.14	SSF	124	9	115	0.60 (0.45-0.76)
PF00916.17	Sulfate_transp	194	41	153	0.60 (0.50-0.70)
PF12821.4	ThrE_2	6	1	5	0.60 (0.60-0.60)
PF03631.12	Virul_fac_BrkB	160	61	99	0.60 (0.51-0.69)
PF05661.9	DUF808	58	20	38	0.60 (0.45-0.74)
PF03600.13	CitMHS	71	9	62	0.60 (0.37-0.82)
PF07786.9	DUF1624	42	10	32	0.60 (0.39-0.80)
PF02447.13	GntP_permease	139	12	127	0.59 (0.44-0.75)
PF01914.14	MarC	77	6	71	0.59 (0.37-0.81)
PF01384.17	PHO4	178	11	167	0.59 (0.39-0.79)
PF03594.10	BenE	13	2	11	0.59 (0.37-0.81)
PF03073.12	TspO_MBR	100	29	71	0.59 (0.48-0.70)
PF04241.12	DUF423	116	43	73	0.59 (0.48-0.70)
PF09335.8	SNARE_assoc	429	51	378	0.59 (0.51-0.67)
PF01554.15	MatE	659	101	558	0.59 (0.53-0.64)
PF02233.13	PNTB	175	29	146	0.58 (0.46-0.71)
PF01618.13	MotA_ExbB	32	14	18	0.58 (0.36-0.81)
PF17113.2	AmpE	7	3	4	0.58 (0.07-1.00)
PF01061.21	ABC2_membrane	328	48	280	0.58 (0.51-0.65)
PF01292.17	Ni_hydr_CYTB	131	58	73	0.57 (0.47-0.67)
PF05232.9	BTP	8	1	7	0.57 (0.57-0.57)
PF01066.18	CDP-OH_P_transf	436	124	312	0.57 (0.51-0.63)
PF00672.22	HAMP	130	40	90	0.57 (0.46-0.67)
PF00892.17	EamA	813	125	688	0.57 (0.51-0.62)
PF07681.9	DoxX	108	47	61	0.56 (0.45-0.67)
PF03547.15	Mem_trans	292	18	274	0.56 (0.40-0.71)
PF01148.17	CTP_transf_1	161	38	123	0.56 (0.45-0.66)
PF03006.17	HlyIII	93	7	86	0.55 (0.35-0.76)
PF00939.16	Na_sulph_symp	109	19	90	0.55 (0.43-0.68)
PF01169.16	UPF0016	92	3	89	0.54 (0.16-0.91)
PF02694.12	UPF0060	21	2	19	0.53 (0.30-0.76)
PF00083.21	Sugar_tr	285	46	239	0.52 (0.43-0.61)
PF01434.15	Peptidase_M41	51	7	44	0.52 (0.34-0.70)
PF02719.12	Polysacc_synt_2	62	19	43	0.52 (0.35-0.69)
PF07947.11	YhhN	64	10	54	0.52 (0.37-0.67)
PF01940.13	DUF92	66	3	63	0.52 (0.26-0.77)
PF00893.16	Multi_Drug_Res	160	7	153	0.52 (0.35-0.68)
PF02628.12	COX15-CtaA	133	50	83	0.52 (0.42-0.61)
PF00507.16	Oxidored_q4	159	4	155	0.51 (0.18-0.85)
PF06580.10	His_kinase	49	9	40	0.51 (0.28-0.74)
PF02040.12	ArsB	26	7	19	0.50 (0.27-0.74)
PF01553.18	Acyltransferase	20	4	16	0.50 (0.12-0.88)
PF03253.11	UT	9	2	7	0.50 (0.00-1.00)
PF06168.8	DUF981	6	2	4	0.50 (0.00-1.00)
PF09997.6	DUF2238	13	5	8	0.50 (0.16-0.84)
PF04304.10	DUF454	69	14	55	0.49 (0.30-0.68)
PF06271.9	RDD	84	20	64	0.49 (0.33-0.66)
PF14667.3	Polysacc_synt_C	181	8	173	0.49 (0.35-0.64)
PF06480.12	FtsH_ext	42	6	36	0.49 (0.32-0.66)
PF02096.17	60KD_IMP	256	43	213	0.49 (0.40-0.57)
PF03806.10	ABG_transport	29	8	21	0.49 (0.25-0.72)
PF07664.9	FeoB_C	103	15	88	0.49 (0.28-0.69)
PF09515.7	Thia_YuaJ	16	6	10	0.48 (0.12-0.85)
PF01595.17	DUF21	238	50	188	0.48 (0.39-0.57)
PF01943.14	Polysacc_synt	189	8	181	0.47 (0.28-0.66)
PF02133.12	Transp_cyt_pur	21	4	17	0.46 (0.11-0.80)
PF03606.12	DcuC	37	4	33	0.45 (0.05-0.86)
PF01773.17	Nucleos_tra2_N	110	18	92	0.44 (0.28-0.61)
PF07662.10	Nucleos_tra2_C	110	18	92	0.44 (0.28-0.61)
PF13807.3	GNVR	25	3	22	0.44 (0.16-0.71)
PF01062.18	Bestrophin	10	2	8	0.44 (0.00-0.90)
PF02163.19	Peptidase_M50	43	4	39	0.44 (0.12-0.75)
PF02706.12	Wzz	34	4	30	0.43 (0.20-0.67)
PF01027.17	Bax1-I	68	16	52	0.42 (0.26-0.58)
PF04235.9	DUF418	7	1	6	0.42 (0.42-0.42)
PF02397.13	Bac_transf	11	1	10	0.40 (0.40-0.40)
PF00953.18	Glycos_transf_4	86	3	83	0.39 (0.18-0.61)
PF01790.15	LGT	75	12	63	0.39 (0.21-0.58)
PF01252.15	Peptidase_A8	63	22	41	0.39 (0.23-0.55)
PF10604.6	Polyketide_cyc2	12	5	7	0.39 (0.11-0.66)
PF07264.8	EI24	73	38	35	0.36 (0.23-0.50)
PF04138.11	GtrA	18	2	16	0.36 (0.00-0.79)
PF17154.1	GAPES3	8	1	7	0.36 (0.36-0.36)
PF07298.8	NnrU	43	5	38	0.35 (0.15-0.56)
PF16401.2	DUF5009	12	3	9	0.35 (0.04-0.66)
PF03609.11	EII-Sor	22	12	10	0.33 (0.10-0.57)
PF12811.4	BaxI_1	20	2	18	0.33 (0.02-0.65)
PF04116.10	FA_hydroxylase	85	7	78	0.31 (0.04-0.59)
PF02417.12	Chromate_transp	8	1	7	0.29 (0.29-0.29)
PF01059.14	Oxidored_q5_N	27	2	25	0.20 (0.00-0.50)
PF06942.9	GlpM	6	5	1	0.20 (0.20-0.20)
PF07331.8	TctB	6	1	5	0.20 (0.20-0.20)
PF06800.9	Sugar_transport	29	2	27	0.19 (0.05-0.33)
PF02654.12	CobS	6	1	5	0.00 (0.00-0.00)
PF06966.9	DUF1295	10	1	9	0.00 (0.00-0.00)

Table 1.3: Predictive performances of the model across protein families. The proteins and performances are with respect to those tested by NYCOMPS as summarized in Figure 1.2.

References

Abell BM, Mullen RT. 2011. Tail-anchored membrane proteins: Exploring the complex diversity of tail-anchored-protein targeting in plant cells. Plant Cell Rep 30:137–151. doi:10.1007/s00299-010-0925-6

Aho K. 2015. Asbio: A collection of statistical tools for biologists.

Almagro Armenteros JJ, Salvatore M, Emanuelsson O, Winther O, von Heijne G, Elofsson A, Nielsen H. 2019. Detecting sequence signals in targeting peptides using deep learning. Life Sci Alliance 2:e201900429. doi:10.26508/lsa.201900429

Almagro Armenteros JJ, Sønderby CK, Sønderby SK, Nielsen H, Winther O. 2017. DeepLoc: Prediction of protein subcellular localization using deep learning. Bioinformatics 33:3387–3395. doi:10.1093/bioinformatics/btx431

Anderson SA, Satyanarayan MB, Wessendorf RL, Lu Y, Fernandez DE. 2021. A homolog of GuidedEntry of Tail-anchored Proteins3 functions in membrane-specific protein targeting in chloroplasts of Arabidopsis. Plant Cell 33:2812–2833. doi:10.1093/plcell/koab145

Anderson SA, Singhal R, Fernandez DE. 2019. Membrane-Specific Targeting of Tail-Anchored Proteins SECE1 and SECE2 Within Chloroplasts. Front Plant Sci 10:1401. doi:10.3389/fpls.2019.01401

Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubin GM, Sherlock G. 2000. Gene ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat Genet 25:25–29. doi:10.1038/75556

Asseck LY, Mehlhorn DG, Monroy JR, Ricardi MM, Breuninger H, Wallmeroth N, Berendzen KW, Nowrousian M, Xing S, Schwappach B, Bayer M, Grefen C. 2021. Endoplasmic reticulum membrane receptors of the GET pathway are conserved throughout eukaryotes. Proc Natl Acad Sci U S A 118:e2017636118. doi:10.1073/pnas.2017636118

Auguie B. 2015. gridExtra: Miscellaneous functions for "Grid" graphics.

Aurora R, Rose GD. 1998. Helix capping. Protein Sci 7:21–38. doi:10.1002/pro.5560070103

Aviram N, Ast T, Costa EA, Arakel EC, Chuartzman SG, Jan CH, Haßdenteufel S, Dudek J, Jung M, Schorr S, Zimmermann R, Schwappach B, Weissman JS, Schuldiner M. 2016. The SND proteins constitute an alternative targeting route to the endoplasmic reticulum. Nature 540:134–138. doi:10.1038/nature20169

Aviram N, Schuldiner M. 2017. Targeting and translocation of proteins to the endoplasmic reticulum at a glance. J Cell Sci 130:4079–4085. doi:10.1242/jcs.204396

Bache SM, Wickham H. 2014. Magrittr: A forward-pipe operator for R.

Bédard J, Kubis S, Bimanadham S, Jarvis P. 2007. Functional similarity between the chloroplast translocon component, Tic40, and the human co-chaperone, Hsp70-interacting protein (Hip). J Biol Chem 282:21404–21414. doi:10.1074/jbc.M611545200

Bédard J, Trösch R, Wu F, Ling Q, Flores-Pérez Ú, Töpel M, Nawaz F, Jarvis P. 2017. Suppressors of the Chloroplast Protein Import Mutant Tic40 Reveal a Genetic Link between Protein Import and Thylakoid Biogenesis. Plant Cell 29:1726–1747. doi:10.1105/tpc.16.00962

Beilharz T, Egan B, Silver PA, Hofmann K, Lithgow T. 2003. Bipartite signals mediate subcellular targeting of tail-anchored membrane proteins in Saccharomyces cerevisiae. J Biol Chem 278:8219–8223. doi:10.1074/jbc.M212725200

Berardini TZ, Reiser L, Li D, Mezheritsky Y, Muller R, Strait E, Huala E. 2015. The Arabidopsis information resource: Making and mining the "gold standard" annotated reference plant genome. Genesis 53:474–485. doi:10.1002/dvg.22877

Berger SA, Krompass D, Stamatakis A. 2011. Performance, accuracy, and Web server for evolutionary placement of short sequence reads under maximum likelihood. Syst Biol 60:291–302. doi:10.1093/sysbio/syr010

Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. 2000. The protein data bank. Nucleic Acids Research 28:235–242.

Bernaudat F, Frelet-Barrand A, Pochon N, Dementin S, Hivin P, Boutigny S, Rioux J-B, Salvi D, Seigneurin-Berny D, Richaud P, Joyard J, Pignol D, Sabaty M, Desnos T, Pebay-Peyroula E, Darrouzet E, Vernet T, Rolland N. 2011. Heterologous expression of membrane proteins: Choosing the appropriate host. PloS One 6:e29191. doi:10.1371/journal.pone.0029191

Bernstein HD, Poritz MA, Strub K, Hoben PJ, Brenner S, Walter P. 1989. Model for signal sequence recognition from amino-acid sequence of 54K subunit of signal recognition particle. Nature 340:482–486. doi:10.1038/340482a0

Bertone P, Kluger Y, Lan N, Zheng D, Christendat D, Yee A, Edwards AM, Arrowsmith CH, Montelione GT, Gerstein M. 2001. SPINE: An integrated tracking database and data mining approach for identifying feasible targets in high-throughput structural proteomics. Nucleic Acids Research 29:2884–2898.

Biebl MM, Buchner J. 2019. Structure, Function, and Regulation of the Hsp90 Machinery. Cold Spring Harb Perspect Biol 11:a034017. doi:10.1101/cshperspect.a034017

Bill RM, Henderson PJF, Iwata S, Kunji ERS, Michel H, Neutze R, Newstead S, Poolman B, Tate CG, Vogel H. 2011. Overcoming barriers to membrane protein structure determination. Nature Biotechnology 29:335–340. doi:10.1038/nbt.1833

Blum M, Chang H-Y, Chuguransky S, Grego T, Kandasaamy S, Mitchell A, Nuka G, Paysan-Lafosse T, Qureshi M, Raj S, Richardson L, Salazar GA, Williams L, Bork P, Bridge A, Gough J, Haft DH, Letunic I, Marchler-Bauer A, Mi H, Natale DA, Necci M, Orengo CA, Pandurangan AP, Rivoire C, Sigrist CJA, Sillitoe I, Thanki N, Thomas PD, Tosatto SCE, Wu CH, Bateman A, Finn RD. 2021. The InterPro protein families and domains database: 20 years on. Nucleic Acids Res 49:D344–D354. doi:10.1093/nar/gkaa977

Bodensohn US, Simm S, Fischer K, Jäschke M, Groß LE, Kramer K, Ehmann C, Rensing SA, Ladig R, Schleiff E. 2019. The intracellular distribution of the components of the GET system in vascular plants. Biochim Biophys Acta Mol Cell Res 1866:1650–1662. doi:10.1016/j.bbamcr.2019.06.012

Bois J. 2020. Justinbois/Bebi103: 0.1.0. doi:10.22002/D1.1615

Borgese N, Colombo S, Pedrazzini E. 2003. The tale of tail-anchored proteins: Coming from the cytosol and looking for a membrane. J Cell Biol 161:1013–1019. doi:10.1083/jcb.200303069

Borkin MA, Gajos KZ, Peters A, Mitsouras D, Melchionna S, Rybicki FJ, Feldman CL, Pfister H. 2011. Evaluation of artery visualizations for heart disease diagnosis. IEEE Trans Vis Comput Graph 17:2479–2488. doi:10.1109/TVCG.2011.192

Borland D, Taylor RM II. 2007. Rainbow Color Map (Still) Considered Harmful. IEEE Comput Grap Appl 27:14–17. doi:10.1109/MCG.2007.323435

Bradley P, Misura KMS, Baker D. 2005. Toward high-resolution de novo structure prediction for small proteins. Science 309:1868–1871. doi:10.1126/science.1113801

Buchanan G, Ricciardelli C, Harris JM, Prescott J, Yu ZC-L, Jia L, Butler LM, Marshall VR, Scher HI, Gerald WL, Coetzee GA, Tilley WD. 2007. Control of androgen receptor signaling in prostate cancer by the cochaperone small glutamine rich tetratricopeptide repeat containing protein alpha. Cancer Res 67:10087–10096. doi:10.1158/0008-5472.CAN-07-1646

Burri L, Lithgow T. 2004. A complete set of SNAREs in yeast. Traffic 5:45–52. doi:10.1046/j.1600-0854.2003.00151.x

Callahan MA, Handley MA, Lee YH, Talbot KJ, Harper JW, Panganiban AT. 1998. Functional interaction of human immunodeficiency virus type 1 Vpu and Gag with a novel member of the tetratricopeptide repeat protein family. J Virol 72:5189–5197. doi:10.1128/JVI.72.6.5189-5197.1998

Canty A, Ripley BD. 2015. Boot: Bootstrap R (S-plus) functions.

Caplan AJ. 2003. What is a co-chaperone? Cell Stress Chaperones 8:105–107. doi:10.1379/1466-1268(2003)008<0105:wiac>2.0.co;2

Chang HC, Nathan DF, Lindquist S. 1997. In vivo analysis of the Hsp90 cochaperone Sti1 (P60). Mol Cell Biol 17:318–325. doi:10.1128/MCB.17.1.318

Chartron JW, Clemons WM, Suloway CJM. 2012a. The complex process of GETting tail-anchored membrane proteins to the ER. Curr Opin Struct Biol 22:217–224. doi:10.1016/j.sbi.2012.03.001

Chartron JW, Gonzalez GM, Clemons WM. 2011. A structural model of the Sgt2 protein and its interactions with chaperones and the Get4/Get5 complex. J Biol Chem 286:34325–34334. doi:10.1074/jbc.M111.277798

Chartron JW, Hunt KCL, Frydman J. 2016. Cotranslational signal-independent SRP preloading during membrane targeting. Nature 536:224–228. doi:10.1038/nature19309

Chartron JW, VanderVelde DG, Clemons WM. 2012b. Structures of the Sgt2/SGTA dimerization domain with the Get5/UBL4A UBL domain reveal an interaction that forms a conserved dynamic interface. Cell Rep 2:1620–1632. doi:10.1016/j.celrep.2012.10.010

Chen CM, Misra TK, Silver S, Rosen BP. 1986. Nucleotide sequence of the structural genes for an anion pump. The plasmid-encoded arsenical resistance operon. J Biol Chem 261:15030–15038.

Chen L, Oughtred R, Berman HM, Westbrook J. 2004. TargetDB: A target registration database for structural genomics projects. Bioinformatics 20:2860–2862. doi:10.1093/bioinformatics/bth300

Chen S, Smith DF. 1998. Hop as an adaptor in the heat shock protein 70 (Hsp70) and Hsp90 chaperone machinery. J Biol Chem 273:35194–35200. doi:10.1074/jbc.273.52.35194

Chio US, Cho H, Shan S-O. 2017. Mechanisms of Tail-Anchored Membrane Protein Targeting and Insertion. Annu Rev Cell Dev Biol 33:417–438. doi:10.1146/annurev-cellbio-100616-060839

Chio US, Chung S, Weiss S, Shan S-O. 2019. A Chaperone Lid Ensures Efficient and Privileged Client Transfer during Tail-Anchored Protein Targeting. Cell Rep 26:37–44.e7. doi:10.1016/j.celrep.2018.12.035

Chitwood PJ, Juszkiewicz S, Guna A, Shao S, Hegde RS. 2018. EMC Is Required to Initiate Accurate Membrane Protein Topogenesis. Cell 175:1507–1519.e16. doi:10.1016/j.cell.2018.10.009

Cho H, Shan S-O. 2018. Substrate relay in an Hsp70-cochaperone cascade safeguards tail-anchored membrane protein targeting. EMBO J 37:e99264. doi:10.15252/embj.201899264

Choi H, Yi T, Ha S-H. 2021. Diversity of Plastid Types and Their Interconversions. Front Plant Sci 12:692024. doi:10.3389/fpls.2021.692024

Chou M-L, Chu C-C, Chen L-J, Akita M, Li H. 2006. Stimulation of transit-peptide release and ATP hydrolysis by a cochaperone during protein import into chloroplasts. J Cell Biol 175:893–900. doi:10.1083/jcb.200609172

Chou M-L, Fitzpatrick LM, Tu S-L, Budziszewski G, Potter-Lewis S, Akita M, Levin JZ, Keegstra K, Li H-M. 2003. Tic40, a membrane-anchored co-chaperone homolog in the chloroplast protein translocon. EMBO J 22:2970–2980. doi:10.1093/emboj/cdg281

Chu R, Takei J, Knowlton JR, Andrykovitch M, Pei W, Kajava AV, Steinbach PJ, Ji X, Bai Y. 2002. Redesign of a four-helix bundle protein by phage display coupled with proteolysis and structural characterization by NMR and X-ray crystallography. J Mol Biol 323:253–262. doi:10.1016/s0022-2836(02)00884-7

Chun E, Thompson AA, Liu W, Roth CB, Griffith MT, Katritch V, Kunken J, Xu F, Cherezov V, Hanson MA, Stevens RC. 2012. Fusion partner toolchest for the stabilization and crystallization of G protein-coupled receptors. Structure 20:967–976. doi:10.1016/j.str.2012.04.010

Clarke E, Sherrill-Mix S. 2015. Ggbeeswarm: Categorical scatter (violin point) plots.

Clemons WM, Gowda K, Black SD, Zwieb C, Ramakrishnan V. 1999. Crystal structure of the conserved subdomain of human protein SRP54M at 2.1 A resolution: Evidence for the mechanism of signal peptide binding. J Mol Biol 292:697–705. doi:10.1006/jmbi.1999.3090

Cock P. 2009. [BioPython] Downloading CDS sequences.

Cock PJA, Antao T, Chang JT, Chapman BA, Cox CJ, Dalke A, Friedberg I, Hamelryck T, Kauff F, Wilczynski B, de Hoon MJL. 2009. Biopython: Freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics 25:1422–1423. doi:10.1093/bioinformatics/btp163

Cole ST, Brosch R, Parkhill J, Garnier T, Churcher C, Harris D, Gordon SV, Eiglmeier K, Gas S, Barry CE, Tekaia F, Badcock K, Basham D, Brown D, Chillingworth T, Connor R, Davies R, Devlin K, Feltwell T, Gentles S, Hamlin N, Holroyd S, Hornsby T, Jagels K, Krogh A, McLean J, Moule S, Murphy L, Oliver K, Osborne J, Quail MA, Rajandream MA, Rogers J, Rutter S, Seeger K, Skelton J, Squares R, Squares S, Sulston JE, Taylor K, Whitehead S, Barrell BG. 1998. Deciphering the biology of Mycobacterium tuberculosis from the complete genome sequence. Nature 393:537–544. doi:10.1038/31159

Coleman JR, Papamichail D, Skiena S, Futcher B, Wimmer E, Mueller S. 2008. Virus attenuation by genome-scale changes in codon pair bias. Science (New York, NY) 320:1784–1787. doi:10.1126/science.1155761

Conklin D, Holderman S, Whitmore TE, Maurer M, Feldhaus AL. 2000. Molecular cloning, chromosome mapping and characterization of UBQLN3 a testis-specific gene that contains an ubiquitin-like domain. Gene 249:91–98. doi:10.1016/s0378-1119(00)00122-0

Costello JL, Castro IG, Camões F, Schrader TA, McNeall D, Yang J, Giannopoulou E-A, Gomes S, Pogenberg V, Bonekamp NA, Ribeiro D, Wilmanns M, Jedd G, Islinger M, Schrader M. 2017. Predicting the targeting of tail-anchored proteins to subcellular compartments in mammalian cells. J Cell Sci 130:1675–1687. doi:10.1242/jcs.200204

Coto ALS, Seraphim TV, Batista FAH, Dores-Silva PR, Barranco ABF, Teixeira FR, Gava LM, Borges JC. 2018. Structural and functional studies of the Leishmania braziliensis SGT co-chaperone indicate that it shares structural features with HIP and can interact with both Hsp90 and Hsp70 with similar affinities. Int J Biol Macromol 118:693–706. doi:10.1016/j.ijbiomac.2018.06.123

Cziepluch C, Kordes E, Poirey R, Grewenig A, Rommelaere J, Jauniaux JC. 1998. Identification of a novel cellular TPR-containing protein, SGT, that interacts with the nonstructural protein NS1 of parvovirus H-1. J Virol 72:4149–4156. doi:10.1128/JVI.72.5.4149-4156.1998

da Fonseca ACC, Matias D, Geraldo LHM, Leser FS, Pagnoncelli I, Garcia C, do Amaral RF, da Rosa BG, Grimaldi I, de Camargo Magalhães ES, Cóppola-Segovia V, de Azevedo EM, Zanata SM, Lima FRS. 2021. The multiple functions of the co-chaperone stress inducible protein 1. Cytokine Growth Factor Rev 57:73–84. doi:10.1016/j.cytogfr.2020.06.003

Daley DO, Rapp M, Granseth E, Melén K, Drew D, von Heijne G. 2005. Global topology analysis of the Escherichia coli inner membrane proteome. Science (New York, NY) 308:1321–1323. doi:10.1126/science.1109730

Dantuma NP, Heinen C, Hoogstraten D. 2009. The ubiquitin receptor Rad23: At the crossroads of nucleotide excision repair and proteasomal degradation. DNA Repair (Amst) 8:449–460. doi:10.1016/j.dnarep.2009.01.005

Darby JF, Krysztofinska EM, Simpson PJ, Simon AC, Leznicki P, Sriskandarajah N, Bishop DS, Hale LR, Alfano C, Conte MR, Martínez-Lumbreras S, Thapaliya A, High S, Isaacson RL. 2014. Solution structure of the SGTA dimerisation domain and investigation of its interactions with the ubiquitin-like domains of BAG6 and UBL4A. PLoS One 9:e113281. doi:10.1371/journal.pone.0113281

DeLong ER, DeLong DM, Clarke-Pearson DL. 1988. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 44:837–845.

Deng H-X, Chen W, Hong S-T, Boycott KM, Gorrie GH, Siddique N, Yang Y, Fecto F, Shi Y, Zhai H, Jiang H, Hirano M, Rampersaud E, Jansen GH, Donkervoort S, Bigio EH, Brooks BR, Ajroud K, Sufit RL, Haines JL, Mugnaini E, Pericak-Vance MA, Siddique T. 2011. Mutations in UBQLN2 cause dominant X-linked juvenile and adult-onset ALS and ALS/dementia. Nature 477:211–215. doi:10.1038/nature10353

Denic V. 2012. A portrait of the GET pathway as a surprisingly complicated young man. Trends Biochem Sci 37:411–417. doi:10.1016/j.tibs.2012.07.004

Dobrogojski J, Adamiec M, Luciński R. 2020. The chloroplast genome: A review. Acta Physiol Plant 42:98. doi:10.1007/s11738-020-03089-x

Dobrovetsky E, Lu ML, Andorn-Broza R, Khutoreskaya G, Bray JE, Savchenko A, Arrowsmith CH, Edwards AM, Koth CM. 2005. High-throughput production of prokaryotic membrane proteins. Journal of Structural and Functional Genomics 6:33–50. doi:10.1007/s10969-005-1363-5

dos Reis M, Wernisch L, Savva R. 2003. Unexpected correlations between gene expression and codon usage bias from microarray data for the whole Escherichia coli K-12 genome. Nucleic Acids Research 31:6976–6985.

Droettboom M. 2016. Change default color map (Fix matplotlib#875).

Drozdetskiy A, Cole C, Procter J, Barton GJ. 2015. JPred4: A protein secondary structure prediction server. Nucleic Acids Res 43:W389–394. doi:10.1093/nar/gkv332

Duncan O, van der Merwe MJ, Daley DO, Whelan J. 2013. The outer mitochondrial membrane in higher plants. Trends Plant Sci 18:207–217. doi:10.1016/j.tplants.2012.12.004

Dupzyk A, Williams JM, Bagchi P, Inoue T, Tsai B. 2017. SGTA-Dependent Regulation of Hsc70 Promotes Cytosol Entry of Simian Virus 40 from the Endoplasmic Reticulum. J Virol 91:e00232–17. doi:10.1128/JVI.00232-17

Dutta S, Tan Y-J. 2008. Structural and functional characterization of human SGT and its interaction with Vpu of the human immunodeficiency virus type 1. Biochemistry 47:10123–10131. doi:10.1021/bi800758a

Dyson HJ, Wright PE. 2004. Unfolded proteins and protein folding studied by NMR. Chem Rev 104:3607–3622. doi:10.1021/cr030403s

Eddins S. 2014. A New Colormap for MATLAB – Part 1 – Introduction. https://blogs.mathworks.com/steve/2014/10/13/a-new-colormap-for-matlab-part-1-introduction/

Eddy SR, Wheeler TJ. 2020. The HMMER development team. HMMER user’s guide: biological sequence analysis using profile hidden markov models.

Eisenberg D, Schwarz E, Komaromy M, Wall R. 1984. Analysis of membrane and surface protein sequences with the hydrophobic moment plot. J Mol Biol 179:125–142. doi:10.1016/0022-2836(84)90309-7

El Ayadi A, Stieren ES, Barral JM, Boehning D. 2013. Ubiquilin-1 and protein quality control in Alzheimer disease. Prion 7:164–169. doi:10.4161/pri.23711

El-Gebali S, Mistry J, Bateman A, Eddy SR, Luciani A, Potter SC, Qureshi M, Richardson LJ, Salazar GA, Smart A, Sonnhammer ELL, Hirsh L, Paladin L, Piovesan D, Tosatto SCE, Finn RD. 2019. The Pfam protein families database in 2019. Nucleic Acids Res 47:D427–D432. doi:10.1093/nar/gky995

Elsasser S, Gali RR, Schwickart M, Larsen CN, Leggett DS, Müller B, Feng MT, Tübing F, Dittmar GAG, Finley D. 2002. Proteasome subunit Rpn1 binds ubiquitin-like protein domains. Nat Cell Biol 4:725–730. doi:10.1038/ncb845

Engelman DM, Steitz TA, Goldman A. 1986. Identifying nonpolar transbilayer helices in amino acid sequences of membrane proteins. Annual Review of Biophysics and Biophysical Chemistry 15:321–353. doi:10.1146/annurev.bb.15.060186.001541

Eshaghi S, Hedrén M, Nasser MIA, Hammarberg T, Thornell A, Nordlund P. 2005. An efficient strategy for high-throughput expression screening of recombinant integral membrane proteins. Protein Science 14:676–683. doi:10.1110/ps.041127005

Fan G-H, Yang W, Sai J, Richmond A. 2002. Hsc/Hsp70 interacting protein (hip) associates with CXCR2 and regulates the receptor signaling and trafficking. J Biol Chem 277:6590–6597. doi:10.1074/jbc.M110588200

Fauchere J, Pliska V. 1983. Hydrophobic parameters II of amino acid side-chains from the partitioning of N-acetyl-amino acid amides. Eur J Med Chem 18.

Fernandez-Patron C, Hardy E, Sosa A, Seoane J, Castellanos L. 1995. Double staining of coomassie blue-stained polyacrylamide gels by imidazole-sodium dodecyl sulfate-zinc reverse staining: Sensitive detection of coomassie blue-undetected proteins. Anal Biochem 224:263–269. doi:10.1006/abio.1995.1039

Figueiredo Costa B, Cassella P, Colombo SF, Borgese N. 2018. Discrimination between the endoplasmic reticulum and mitochondria by spontaneously inserting tail-anchored proteins. Traffic 19:182–197. doi:10.1111/tra.12550

Finn RD, Bateman A, Clements J, Coggill P, Eberhardt RY, Eddy SR, Heger A, Hetherington K, Holm L, Mistry J, Sonnhammer ELL, Tate J, Punta M. 2014. Pfam: The protein families database. Nucleic Acids Research 42:D222–230. doi:10.1093/nar/gkt1223

Finn RD, Coggill P, Eberhardt RY, Eddy SR, Mistry J, Mitchell AL, Potter SC, Punta M, Qureshi M, Sangrador-Vegas A, Salazar GA, Tate J, Bateman A. 2016. The Pfam protein families database: Towards a more sustainable future. Nucleic Acids Res 44:D279–285. doi:10.1093/nar/gkv1344

Fishbain S, Prakash S, Herrig A, Elsasser S, Matouschek A. 2011. Rad23 escapes degradation because it lacks a proteasome initiation region. Nat Commun 2:192. doi:10.1038/ncomms1194

Fluman N, Navon S, Bibi E, Pilpel Y. 2014. mRNA-programmed translation pauses in the targeting of E. Coli membrane proteins. eLife 3. doi:10.7554/eLife.03440

Fowler DM, Fields S. 2014. Deep mutational scanning: A new style of protein science. Nat Methods 11:801–807. doi:10.1038/nmeth.3027

Frain KM, Gangl D, Jones A, Zedler JAZ, Robinson C. 2016. Protein translocation and thylakoid biogenesis in cyanobacteria. Biochim Biophys Acta 1857:266–273. doi:10.1016/j.bbabio.2015.08.010

Franklin M. 2013. [Phenixbb] coot and mtz interpretation.

Freedman D, Diaconis P. 1981. On the histogram as a density estimator:L 2 theory. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 57:453–476. doi:10.1007/BF01025868

Fry MY, Clemons WM. 2018. Complexity in targeting membrane proteins. Science 359:390–391. doi:10.1126/science.aar5992

Fry MY, Najdrová V, Maggiolo AO, Saladi SM, Doležal P, Clemons WM. 2022. Structurally derived universal mechanism for the catalytic cycle of the tail-anchored targeting factor Get3. Nat Struct Mol Biol 29:820–830. doi:10.1038/s41594-022-00798-4

Fry MY, Saladi SM, Cunha A, Clemons WM. 2021. Sequence-based features that are determinant for tail-anchored membrane protein sorting in eukaryotes. Traffic 22:306–318. doi:10.1111/tra.12809

Gabanyi MJ, Adams PD, Arnold K, Bordoli L, Carter LG, Flippen-Andersen J, Gifford L, Haas J, Kouranov A, McLaughlin WA, Micallef DI, Minor W, Shah R, Schwede T, Tao Y-P, Westbrook JD, Zimmerman M, Berman HM. 2011. The Structural Biology Knowledgebase: A portal to protein structures, sequences, functions, and methods. Journal of Structural and Functional Genomics 12:45–54. doi:10.1007/s10969-011-9106-2

Gamble CE, Brule CE, Dean KM, Fields S, Grayhack EJ. 2016. Adjacent codons act in concert to modulate translation efficiency in yeast. Cell 166:679–690. doi:10.1016/j.cell.2016.05.070

Garnier S. 2016. Viridis: Default color maps from ’matplotlib’.

Gautier R, Douguet D, Antonny B, Drin G. 2008. HELIQUEST: A web server to screen sequences with specific alpha-helical properties. Bioinformatics 24:2101–2102. doi:10.1093/bioinformatics/btn392

Geertsma ER, Groeneveld M, Slotboom D-J, Poolman B. 2008. Quality control of overexpressed membrane proteins. Proceedings of the National Academy of Sciences of the United States of America 105:5722–5727. doi:10.1073/pnas.0802190105

Gelvin SB. 2017. Integration of Agrobacterium T-DNA into the Plant Genome. Annu Rev Genet 51:195–217. doi:10.1146/annurev-genet-120215-035320

Gene Ontology Consortium. 2021. The Gene Ontology resource: Enriching a GOld mine. Nucleic Acids Res 49:D325–D334. doi:10.1093/nar/gkaa1113

Gibson DG, Young L, Chuang R-Y, Venter JC, Hutchison CA, Smith HO. 2009. Enzymatic assembly of DNA molecules up to several hundred kilobases. Nat Methods 6:343–345. doi:10.1038/nmeth.1318

Goodman DB, Church GM, Kosuri S. 2013. Causes and effects of N-terminal codon bias in bacterial genes. Science (New York, NY) 342:475–479. doi:10.1126/science.1241934

Gordon E, Horsefield R, Swarts HGP, de Pont JJHHM, Neutze R, Snijder A. 2008. Effective high-throughput overproduction of membrane proteins in Escherichia coli. Protein Expression and Purification 62:1–8. doi:10.1016/j.pep.2008.07.005

Graether SP. 2018. Troubleshooting Guide to Expressing Intrinsically Disordered Proteins for Use in NMR Experiments. Front Mol Biosci 5:118. doi:10.3389/fmolb.2018.00118

Gristick HB, Rao M, Chartron JW, Rome ME, Shan S-O, Clemons WM. 2014. Crystal structure of ATP-bound Get3-Get4-Get5 complex reveals regulation of Get3 by Get4. Nat Struct Mol Biol 21:437–442. doi:10.1038/nsmb.2813

Guna A, Hegde RS. 2018. Transmembrane Domain Recognition during Membrane Protein Biogenesis and Quality Control. Curr Biol 28:R498–R511. doi:10.1016/j.cub.2018.02.004

Guna A, Volkmar N, Christianson JC, Hegde RS. 2018. The ER membrane protein complex is a transmembrane domain insertase. Science 359:470–473. doi:10.1126/science.aao3099

Hara T, Kamura T, Kotoshiba S, Takahashi H, Fujiwara K, Onoyama I, Shirakawa M, Mizushima N, Nakayama KI. 2005. Role of the UBL-UBA protein KPC2 in degradation of P27 at G1 phase of the cell cycle. Mol Cell Biol 25:9292–9303. doi:10.1128/MCB.25.21.9292-9303.2005

Harrower M, Brewer CA. 2003. ColorBrewer.org: An online tool for selecting colour schemes for maps. Cartographic Journal, The 40:27–37.

Hartley AM, Lukoyanova N, Zhang Y, Cabrera-Orefice A, Arnold S, Meunier B, Pinotsis N, Maréchal A. 2019. Structure of yeast cytochrome c oxidase in a supercomplex with cytochrome Bc1. Nat Struct Mol Biol 26:78–83. doi:10.1038/s41594-018-0172-z

Hegde RS, Keenan RJ. 2022. The mechanisms of integral membrane protein biogenesis. Nat Rev Mol Cell Biol 23:107–124. doi:10.1038/s41580-021-00413-2

Hegde RS, Keenan RJ. 2011. Tail-anchored membrane protein insertion into the endoplasmic reticulum. Nat Rev Mol Cell Biol 12:787–798. doi:10.1038/nrm3226

Hendrickson WA. 2016. Atomic-level analysis of membrane-protein structure. Nature Structural & Molecular Biology 23:464–467. doi:10.1038/nsmb.3215

Hessa T, Meindl-Beinker NM, Bernsel A, Kim H, Sato Y, Lerch-Bader M, Nilsson I, White SH, von Heijne G. 2007. Molecular code for transmembrane-helix recognition by the Sec61 translocon. Nature 450:1026–1030. doi:10.1038/nature06387

Hessa T, Sharma A, Mariappan M, Eshleman HD, Gutierrez E, Hegde RS. 2011. Protein targeting and degradation are coupled for elimination of mislocalized proteins. Nature 475:394–397. doi:10.1038/nature10181

Howe KL, Contreras-Moreira B, De Silva N, Maslen G, Akanni W, Allen J, Alvarez-Jarreta J, Barba M, Bolser DM, Cambell L, Carbajo M, Chakiachvili M, Christensen M, Cummins C, Cuzick A, Davis P, Fexova S, Gall A, George N, Gil L, Gupta P, Hammond-Kosack KE, Haskell E, Hunt SE, Jaiswal P, Janacek SH, Kersey PJ, Langridge N, Maheswari U, Maurel T, McDowall MD, Moore B, Muffato M, Naamati G, Naithani S, Olson A, Papatheodorou I, Patricio M, Paulini M, Pedro H, Perry E, Preece J, Rosello M, Russell M, Sitnik V, Staines DM, Stein J, Tello-Ruiz MK, Trevanion SJ, Urban M, Wei S, Ware D, Williams G, Yates AD, Flicek P. 2020. Ensembl Genomes 2020-enabling non-vertebrate genomic research. Nucleic Acids Res 48:D689–D695. doi:10.1093/nar/gkz890

Itakura E, Zavodszky E, Shao S, Wohlever ML, Keenan RJ, Hegde RS. 2016. Ubiquilins Chaperone and Triage Mitochondrial Membrane Proteins for Degradation. Mol Cell 63:21–33. doi:10.1016/j.molcel.2016.05.020

Jahandideh S, Jaroszewski L, Godzik A. 2014. Improving the chances of successful protein structure determination with a random forest classifier. Acta Crystallographica Section D, Biological Crystallography 70:627–635. doi:10.1107/S1399004713032070

Jenny B. 2020. Color Oracle: Design for the Color Impaired.

Joachims T. 2002. Optimizing search engines using clickthrough data. ACM Press. p. 133. doi:10.1145/775047.775067

Johansson LC, Stauch B, Ishchenko A, Cherezov V. 2017. A bright future for serial femtosecond crystallography with XFELs. Trends in Biochemical Sciences 42:749–762. doi:10.1016/j.tibs.2017.06.007

Kabsch W, Sander C. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22:2577–2637. doi:10.1002/bip.360221211

Kajander T, Sachs JN, Goldman A, Regan L. 2009. Electrostatic interactions of Hsp-organizing protein tetratricopeptide domains with Hsp70 and Hsp90: Computational analysis and protein engineering. J Biol Chem 284:25364–25374. doi:10.1074/jbc.M109.033894

Kalbfleisch T, Cambon A, Wattenberg BW. 2007. A bioinformatics approach to identifying tail-anchored proteins in the human genome. Traffic 8:1687–1694. doi:10.1111/j.1600-0854.2007.00661.x

Käll L, Krogh A, Sonnhammer ELL. 2004. A combined transmembrane topology and signal peptide prediction method. Journal of Molecular Biology 338:1027–1036. doi:10.1016/j.jmb.2004.03.016

Katoh K, Standley DM. 2013. MAFFT multiple sequence alignment software version 7: Improvements in performance and usability. Mol Biol Evol 30:772–780. doi:10.1093/molbev/mst010

Keenan RJ, Freymann DM, Walter P, Stroud RM. 1998. Crystal structure of the signal sequence binding subunit of the signal recognition particle. Cell 94:181–191. doi:10.1016/s0092-8674(00)81418-x

Kendall MG. 1938. A new measure of rank correlation. Biometrika 30:81. doi:10.2307/2332226

Kiktev DA, Patterson JC, Müller S, Bariar B, Pan T, Chernoff YO. 2012. Regulation of chaperone effects on a yeast prion by cochaperone Sgt2. Mol Cell Biol 32:4960–4970. doi:10.1128/MCB.00875-12

Kirschke E, Goswami D, Southworth D, Griffin PR, Agard DA. 2014. Glucocorticoid receptor function regulated by coordinated action of the Hsp90 and Hsp70 chaperone cycles. Cell 157:1685–1697. doi:10.1016/j.cell.2014.04.038

Ko HS, Uehara T, Tsuruma K, Nomura Y. 2004. Ubiquilin interacts with ubiquitylated proteins and proteasome through its ubiquitin-associated and ubiquitin-like domains. FEBS Lett 566:110–114. doi:10.1016/j.febslet.2004.04.031

Ko K, Banerjee S, Innes J, Taylor D, Ko Z. 2004. The Tic40 translocon components exhibit preferential interactions with different forms of the Oee1 plastid protein precursor. Funct Plant Biol 31:285–294. doi:10.1071/FP03195

Köhler RH. 1998. GFP for in vivo imaging of subcellular structures in plant cells. Trends in Plant Science 3:317–320. doi:10.1016/S1360-1385(98)01276-X

Koonin EV. 1993. A superfamily of ATPases with diverse functions containing either classical or deviant ATP-binding motif. J Mol Biol 229:1165–1174. doi:10.1006/jmbi.1993.1115

Korepanova A, Gao FP, Hua Y, Qin H, Nakamoto RK, Cross TA. 2005. Cloning and expression of multiple integral membrane proteins from Mycobacterium tuberculosis in Escherichia coli. Protein Science 14:148–158. doi:10.1110/ps.041022305

Kotoshiba S, Kamura T, Hara T, Ishida N, Nakayama KI. 2005. Molecular dissection of the interaction between P27 and Kip1 ubiquitylation-promoting complex, the ubiquitin ligase that regulates proteolysis of P27 in G1 phase. J Biol Chem 280:17694–17700. doi:10.1074/jbc.M500866200

Kovacheva S, Bédard J, Patel R, Dudley P, Twell D, Ríos G, Koncz C, Jarvis P. 2005. In vivo studies on the roles of Tic110, Tic40 and Hsp93 during chloroplast protein import. Plant J 41:412–428. doi:10.1111/j.1365-313X.2004.02307.x

Kovalevskiy O, Nicholls RA, Long F, Carlon A, Murshudov GN. 2018. Overview of refinement procedures within REFMAC5: Utilizing data from different sources. Acta Crystallogr D Struct Biol 74:215–227. doi:10.1107/S2059798318000979

Kovesi P. 2015. Good Colour Maps: How to Design Them.

Krogh A, Larsson B, von Heijne G, Sonnhammer EL. 2001. Predicting transmembrane protein topology with a hidden Markov model: Application to complete genomes. J Mol Biol 305:567–580. doi:10.1006/jmbi.2000.4315

Kuhn M. 2008. Building predictive models in R using the caret package. J of Stat Soft.

Kunze M, Berger J. 2015. The similarity between N-terminal targeting signals for protein import into different organelles and its evolutionary relevance. Front Physiol 6:259. doi:10.3389/fphys.2015.00259

Kutay U, Hartmann E, Rapoport TA. 1993. A class of membrane proteins with a C-terminal anchor. Trends Cell Biol 3:72–75. doi:10.1016/0962-8924(93)90066-a

Kyte J, Doolittle RF. 1982. A simple method for displaying the hydropathic character of a protein. J Mol Biol 157:105–132. doi:10.1016/0022-2836(82)90515-0

Lässle M, Blatch GL, Kundra V, Takatori T, Zetter BR. 1997. Stress-inducible, murine protein mSTI1. Characterization of binding domains for heat shock proteins and in vitro phosphorylation by different kinases. J Biol Chem 272:1876–1884. doi:10.1074/jbc.272.3.1876

Lechat P, Hummel L, Rousseau S, Moszer I. 2008. GenoList: An integrated environment for comparative analysis of microbial genomes. Nucleic Acids Research 36:D469–474. doi:10.1093/nar/gkm1042

Lee DW, Lee J, Hwang I. 2017. Sorting of nuclear-encoded chloroplast membrane proteins. Curr Opin Plant Biol 40:1–7. doi:10.1016/j.pbi.2017.06.011

Leipe DD, Wolf YI, Koonin EV, Aravind L. 2002. Classification and evolution of P-loop GTPases and related ATPases. J Mol Biol 317:41–72. doi:10.1006/jmbi.2001.5378

Letunic I, Bork P. 2018. 20 years of the SMART protein domain annotation resource. Nucleic Acids Res 46:D493–D496. doi:10.1093/nar/gkx922

Letunic I, Doerks T, Bork P. 2015. SMART: Recent updates, new developments and status in 2015. Nucleic Acids Res 43:D257–260. doi:10.1093/nar/gku949

Levchenko M, Wuttke J-M, Römpler K, Schmidt B, Neifer K, Juris L, Wissel M, Rehling P, Deckers M. 2016. Cox26 is a novel stoichiometric subunit of the yeast cytochrome c oxidase. Biochim Biophys Acta 1863:1624–1632. doi:10.1016/j.bbamcr.2016.04.007

Lewinson O, Lee AT, Rees DC. 2008. The funnel approach to the precrystallization production of membrane proteins. Journal of Molecular Biology 377:62–73. doi:10.1016/j.jmb.2007.12.059

Leznicki P, High S. 2012. SGTA antagonizes BAG6-mediated protein triage. Proc Natl Acad Sci U S A 109:19214–19219. doi:10.1073/pnas.1209997109

Leznicki P, Korac-Prlic J, Kliza K, Husnjak K, Nyathi Y, Dikic I, High S. 2015. Binding of SGTA to Rpn13 selectively modulates protein quality control. J Cell Sci 128:3187–3196. doi:10.1242/jcs.165209

Li G-W, Oh E, Weissman JS. 2012. The anti-Shine-Dalgarno sequence drives translational pausing and codon choice in bacteria. Nature 484:538–541. doi:10.1038/nature10965

Li W, Godzik A. 2006. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics 22:1658–1659. doi:10.1093/bioinformatics/btl158

Li Z, Hartl FU, Bracher A. 2013. Structure and function of Hip, an attenuator of the Hsp70 chaperone cycle. Nat Struct Mol Biol 20:929–935. doi:10.1038/nsmb.2608

Liebschner D, Afonine PV, Baker ML, Bunkóczi G, Chen VB, Croll TI, Hintze B, Hung L-W, Jain S, McCoy AJ, Moriarty NW, Oeffner RD, Poon BK, Prisant MG, Read RJ, Richardson JS, Richardson DC, Sammito MD, Sobolev OV, Stockwell DH, Terwilliger TC, Urzhumtsev AG, Videau LL, Williams CJ, Adams PD. 2019. Macromolecular structure determination using X-rays, neutrons and electrons: Recent developments in Phenix. Acta Crystallogr D Struct Biol 75:861–877. doi:10.1107/S2059798319011471

Lim PJ, Danner R, Liang J, Doong H, Harman C, Srinivasan D, Rothenberg C, Wang H, Ye Y, Fang S, Monteiro MJ. 2009. Ubiquilin and P97/VCP bind erasin, forming a complex involved in ERAD. J Cell Biol 187:201–217. doi:10.1083/jcb.200903024

Lin K-F, Fry MY, Saladi SM, Clemons WM. 2021. Molecular basis of tail-anchored integral membrane protein recognition by the cochaperone Sgt2. J Biol Chem 296:100441. doi:10.1016/j.jbc.2021.100441

Linding R, Jensen LJ, Diella F, Bork P, Gibson TJ, Russell RB. 2003. Protein disorder prediction: Implications for structural proteomics. Structure 11:1453–1459.

Liou S-T, Wang C. 2005. Small glutamine-rich tetratricopeptide repeat-containing protein is composed of three structural units with distinct functions. Arch Biochem Biophys 435:253–263. doi:10.1016/j.abb.2004.12.020

Liu FH, Wu SJ, Hu SM, Hsiao CD, Wang C. 1999. Specific interaction of the 70-kDa heat shock cognate protein with the tetratricopeptide repeats. J Biol Chem 274:34425–34432. doi:10.1074/jbc.274.48.34425

Long P, Samnakay P, Jenner P, Rose S. 2012. A yeast two-hybrid screen reveals that osteopontin associates with MAP1A and MAP1B in addition to other proteins linked to microtubule stability, apoptosis and protein degradation in the human brain. Eur J Neurosci 36:2733–2742. doi:10.1111/j.1460-9568.2012.08189.x

Lorenz R, Bernhart SH, Höner Zu Siederdissen C, Tafer H, Flamm C, Stadler PF, Hofacker IL. 2011. ViennaRNA package 2.0. Algorithms for molecular biology: AMB 6:26. doi:10.1186/1748-7188-6-26

Lott A, Oroz J, Zweckstetter M. 2020. Molecular basis of the interaction of Hsp90 with its co-chaperone Hop. Protein Sci 29:2422–2432. doi:10.1002/pro.3969

Love J, Mancia F, Shapiro L, Punta M, Rost B, Girvin M, Wang D-N, Zhou M, Hunt JF, Szyperski T, Gouaux E, MacKinnon R, McDermott A, Honig B, Inouye M, Montelione G, Hendrickson WA. 2010. The New York Consortium on Membrane Protein Structure (NYCOMPS): A high-throughput platform for structural genomics of integral membrane proteins. Journal of Structural and Functional Genomics 11:191–199. doi:10.1007/s10969-010-9094-7

Lowe ED, Hasan N, Trempe JF, Fonso L, Noble MEM, Endicott JA, Johnson LN, Brown NR. 2006. Structures of the Dsk2 UBL and UBA domains and their complex. Acta Crystallogr D Biol Crystallogr 62:177–188. doi:10.1107/S0907444905037777

Lu AX, Zarin T, Hsu IS, Moses AM. 2019. YeastSpotter: Accurate and parameter-free web segmentation for microscopy images of yeast cells. Bioinformatics 35:4525–4527. doi:10.1093/bioinformatics/btz402

Lundstrom K, Wagner R, Reinhart C, Desmyter A, Cherouati N, Magnin T, Zeder-Lutz G, Courtot M, Prual C, André N, Hassaine G, Michel H, Cambillau C, Pattus F. 2006. Structural genomics on membrane proteins: Comparison of more than 100 GPCRs in 3 expression systems. Journal of Structural and Functional Genomics 7:77–91. doi:10.1007/s10969-006-9011-2

Luo P, Baldwin RL. 1997. Mechanism of helix induction by trifluoroethanol: A framework for extrapolating the helix-forming properties of peptides from trifluoroethanol/water mixtures back to water. Biochemistry 36:8413–8421. doi:10.1021/bi9707133

Ma P, Varela F, Magoch M, Silva AR, Rosário AL, Brito J, Oliveira TF, Nogly P, Pessanha M, Stelter M, Kletzin A, Henderson PJF, Archer M. 2013. An efficient strategy for small-scale screening and production of archaeal membrane transport proteins in Escherichia coli. PloS One 8:e76913. doi:10.1371/journal.pone.0076913

Machado GM, Oliveira MM, Fernandes L. 2009. A Physiologically-based Model for Simulation of Color Vision Deficiency. IEEE Trans Visual Comput Graphics 15:1291–1298. doi:10.1109/TVCG.2009.113

Madhavan V, Bhatt F, Jeffery CJ. 2010. Recombinant expression screening of P. Aeruginosa bacterial inner membrane proteins. BMC biotechnology 10:83. doi:10.1186/1472-6750-10-83

Maggiolo AO, Mahajan S, Rees DC, Clemons WM. 2023. Intradimeric Walker A ATPases: Conserved Features of A Functionally Diverse Family. J Mol Biol 167965. doi:10.1016/j.jmb.2023.167965

Manu MS, Ghosh D, Chaudhari BP, Ramasamy S. 2018. Analysis of tail-anchored protein translocation pathway in plants. Biochem Biophys Rep 14:161–167. doi:10.1016/j.bbrep.2018.05.001

Mareš J, Strunecký O, Bučinská L, Wiedermannová J. 2019. Evolutionary Patterns of Thylakoid Architecture in Cyanobacteria. Front Microbiol 10:277. doi:10.3389/fmicb.2019.00277

Marín I. 2014. The ubiquilin gene family: Evolutionary patterns and functional insights. BMC Evol Biol 14:63. doi:10.1186/1471-2148-14-63

Marshall SS, Niesen MJM, Müller A, Tiemann K, Saladi SM, Galimidi RP, Zhang B, Clemons WM, Miller TF. 2016. A link between integral membrane protein expression and simulated integration efficiency. Cell Reports 16:2169–2177. doi:10.1016/j.celrep.2016.07.042

Martínez-Lumbreras S, Krysztofinska EM, Thapaliya A, Spilotros A, Matak-Vinkovic D, Salvadori E, Roboti P, Nyathi Y, Muench JH, Roessler MM, Svergun DI, High S, Isaacson RL. 2018. Structural complexity of the co-chaperone SGTA: A conserved C-terminal region is implicated in dimerization and substrate quality control. BMC Biol 16:76. doi:10.1186/s12915-018-0542-3

Martins VR, Graner E, Garcia-Abreu J, de Souza SJ, Mercadante AF, Veiga SS, Zanata SM, Neto VM, Brentani RR. 1997. Complementary hydropathy identifies a cellular prion protein receptor. Nat Med 3:1376–1382. doi:10.1038/nm1297-1376

Mateja A, Szlachcic A, Downing ME, Dobosz M, Mariappan M, Hegde RS, Keenan RJ. 2009. The structural basis of tail-anchored membrane protein recognition by Get3. Nature 461:361–366. doi:10.1038/nature08319

McGibbon RT, Beauchamp KA, Harrigan MP, Klein C, Swails JM, Hernández CX, Schwantes CR, Wang L-P, Lane TJ, Pande VS. 2015. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys J 109:1528–1532. doi:10.1016/j.bpj.2015.08.015

McMurdie PJ, Holmes S. 2013. Phyloseq: An R package for reproducible interactive analysis and graphics of microbiome census data. PLoS One 8:e61217. doi:10.1371/journal.pone.0061217

Merk A, Bartesaghi A, Banerjee S, Falconieri V, Rao P, Davis MI, Pragani R, Boxer MB, Earl LA, Milne JLS, Subramaniam S. 2016. Breaking cryo-EM resolution barriers to facilitate drug discovery. Cell 165:1698–1707. doi:10.1016/j.cell.2016.05.040

Micsonai A, Wien F, Kernya L, Lee Y-H, Goto Y, Réfrégiers M, Kardos J. 2015. Accurate secondary structure prediction and fold recognition for circular dichroism spectroscopy. Proc Natl Acad Sci U S A 112:E3095–3103. doi:10.1073/pnas.1500851112

Mirzadeh K, Martínez V, Toddo S, Guntur S, Herrgård MJ, Elofsson A, Nørholm MHH, Daley DO. 2015. Enhanced protein production in escherichia coli by optimization of cloning scars at the vector-coding sequence junction. ACS synthetic biology. doi:10.1021/acssynbio.5b00033

Mistry J, Chuguransky S, Williams L, Qureshi M, Salazar GA, Sonnhammer ELL, Tosatto SCE, Paladin L, Raj S, Richardson LJ, Finn RD, Bateman A. 2021. Pfam: The protein families database in 2021. Nucleic Acids Res 49:D412–D419. doi:10.1093/nar/gkaa913

Mock J-Y, Chartron JW, Zaslaver M, Xu Y, Ye Y, Clemons WM. 2015. Bag6 complex contains a minimal tail-anchor-targeting module and a mock BAG domain. Proc Natl Acad Sci U S A 112:106–111. doi:10.1073/pnas.1402745112

Moore KR, Magnabosco C, Momper L, Gold DA, Bosak T, Fournier GP. 2019. An Expanded Ribosomal Phylogeny of Cyanobacteria Supports a Deep Placement of Plastids. Front Microbiol 10:1612. doi:10.3389/fmicb.2019.01612

Moreland K. 2016. Why we use bad color maps and what you can do about it. Electronic Imaging 2016:1–6. doi:10.2352/ISSN.2470-1173.2016.16.HVEI-133

Moroney N, Fairchild MD, Hunt RW, Li C, Luo MR, Newman T. 2002. The CIECAM02 color appearance modelColor and Imaging Conference. Society for Imaging Science and Technology. pp. 23–27.

Nannenga BL, Gonen T. 2016. MicroED opens a new era for biological structure determination. Current Opinion in Structural Biology 40:128–135. doi:10.1016/j.sbi.2016.09.007

Nelson GM, Huffman H, Smith DF. 2003. Comparison of the carboxy-terminal DP-repeat region in the co-chaperones Hop and Hip. Cell Stress Chaperones 8:125–133. doi:10.1379/1466-1268(2003)008<0125:cotcdr>2.0.co;2

Nelson KE, Clayton RA, Gill SR, Gwinn ML, Dodson RJ, Haft DH, Hickey EK, Peterson JD, Nelson WC, Ketchum KA, McDonald L, Utterback TR, Malek JA, Linher KD, Garrett MM, Stewart AM, Cotton MD, Pratt MS, Phillips CA, Richardson D, Heidelberg J, Sutton GG, Fleischmann RD, Eisen JA, White O, Salzberg SL, Smith HO, Venter JC, Fraser CM. 1999. Evidence for lateral gene transfer between Archaea and bacteria from genome sequence of Thermotoga maritima. Nature 399:323–329. doi:10.1038/20601

Neuwirth E. 2014. RColorBrewer: ColorBrewer palettes.

Nielsen H. 2017. Predicting Secretory Proteins with SignalP. Methods Mol Biol 1611:59–73. doi:10.1007/978-1-4939-7015-5_6

Niesen MJM, Marshall SS, Miller TF, Clemons WM. 2017. Improving membrane protein expression by optimizing integration efficiency. The Journal of Biological Chemistry. doi:10.1074/jbc.M117.813469

Nørholm MHH, Light S, Virkki MTI, Elofsson A, von Heijne G, Daley DO. 2012. Manipulating the genetic code for membrane protein production: What have we learnt so far? Biochimica et biophysica acta 1818:1091–1096. doi:10.1016/j.bbamem.2011.08.018

Nørholm MHH, Toddo S, Virkki MTI, Light S, von Heijne G, Daley DO. 2013. Improved production of membrane proteins in Escherichia coli by selective codon substitutions. FEBS letters 587:2352–2358. doi:10.1016/j.febslet.2013.05.063

Nuñez JR, Anderton CR, Renslow RS. 2018. Optimizing colormaps with consideration for color vision deficiency to enable accurate interpretation of scientific data. PLoS ONE 13:e0199239. doi:10.1371/journal.pone.0199239

Oborník M. 2019. Endosymbiotic Evolution of Algae, Secondary Heterotrophy and Parasitism. Biomolecules 9:266. doi:10.3390/biom9070266

Okabe M, Ito K. 2002. How to make figures and presentations that are friendly to color blind people. http://jfly.iam.u-tokyo.ac.jp/html/color_blind/

Okreglak V, Walter P. 2014. The conserved AAA-ATPase Msp1 confers organelle specificity to tail-anchored proteins. Proc Natl Acad Sci U S A 111:8019–8024. doi:10.1073/pnas.1405755111

Onuoha SC, Coulstock ET, Grossmann JG, Jackson SE. 2008. Structural studies on the co-chaperone Hop and its complexes with Hsp90. J Mol Biol 379:732–744. doi:10.1016/j.jmb.2008.02.013

Pace CN, Scholtz JM. 1998. A helix propensity scale based on experimental studies of peptides and proteins. Biophys J 75:422–427. doi:10.1016/s0006-3495(98)77529-0

Pattengale ND, Alipour M, Bininda-Emonds ORP, Moret BME, Stamatakis A. 2010. How many bootstrap replicates are necessary? J Comput Biol 17:337–354. doi:10.1089/cmb.2009.0179

Peden JF. 2000. Analysis of codon usage (PhD thesis). University of Nottingham.

Pei J, Kim B-H, Grishin NV. 2008. PROMALS3D: A tool for multiple protein sequence and structure alignments. Nucleic Acids Res 36:2295–2300. doi:10.1093/nar/gkn072

Petrovskaya LE, Shulga AA, Bocharova OV, Ermolyuk YS, Kryukova EA, Chupin VV, Blommers MJJ, Arseniev AS, Kirpichnikov MP. 2010. Expression of G-protein coupled receptors in Escherichia coli for structural studies. Biochemistry (Moscow) 75:881–891.

Pettersen EF, Goddard TD, Huang CC, Meng EC, Couch GS, Croll TI, Morris JH, Ferrin TE. 2021. UCSF ChimeraX : Structure visualization for researchers, educators, and developers. Protein Science 30:70–82. doi:10.1002/pro.3943

Pieper U, Schlessinger A, Kloppmann E, Chang GA, Chou JJ, Dumont ME, Fox BG, Fromme P, Hendrickson WA, Malkowski MG, Rees DC, Stokes DL, Stowell MHB, Wiener MC, Rost B, Stroud RM, Stevens RC, Sali A. 2013. Coordinating the impact of structural genomics on the human a-helical transmembrane proteome. Nat Struct Mol Biol 20:135–138. doi:10.1038/nsmb.2508

Pierce BG, Wiehe K, Hwang H, Kim B-H, Vreven T, Weng Z. 2014. ZDOCK server: Interactive docking prediction of protein-protein complexes and symmetric multimers. Bioinformatics 30:1771–1773. doi:10.1093/bioinformatics/btu097

Prapapanich V, Chen S, Smith DF. 1998. Mutation of Hip’s carboxy-terminal region inhibits a transitional stage of progesterone receptor assembly. Mol Cell Biol 18:944–952. doi:10.1128/MCB.18.2.944

Prapapanich V, Chen S, Toran EJ, Rimerman RA, Smith DF. 1996. Mutational analysis of the Hsp70-interacting protein Hip. Mol Cell Biol 16:6200–6207. doi:10.1128/MCB.16.11.6200

Price WN, Chen Y, Handelman SK, Neely H, Manor P, Karlin R, Nair R, Liu J, Baran M, Everett J, Tong SN, Forouhar F, Swaminathan SS, Acton T, Xiao R, Luft JR, Lauricella A, DeTitta GT, Rost B, Montelione GT, Hunt JF. 2009. Understanding the physical properties that control protein crystallization by analysis of large-scale experimental data. Nature Biotechnology 27:51–57. doi:10.1038/nbt.1514

Prodromou C. 2016. Mechanisms of Hsp90 regulation. Biochem J 473:2439–2452. doi:10.1042/BCJ20160005

Psakis G, Nitschkowski S, Holz C, Kress D, Maestre-Reyna M, Polaczek J, Illing G, Essen L-O. 2007. Expression screening of integral membrane proteins from Helicobacter pylori 26695. Protein Science 16:2667–2676. doi:10.1110/ps.073104707

Punta M, Love J, Handelman S, Hunt JF, Shapiro L, Hendrickson WA, Rost B. 2009. Structural genomics target selection for the New York consortium on membrane protein structure. Journal of Structural and Functional Genomics 10:255–268. doi:10.1007/s10969-009-9071-1

R Core Team. 2015. R: A Language and Environment for Statistical Computing.

Rabu C, Schmid V, Schwappach B, High S. 2009. Biogenesis of tail-anchored proteins: The beginning for the end? J Cell Sci 122:3605–3612. doi:10.1242/jcs.041210

Rao M, Okreglak V, Chio US, Cho H, Walter P, Shan S-O. 2016. Multiple selection filters ensure accurate tail-anchored membrane protein targeting. Elife 5:e21301. doi:10.7554/eLife.21301

Raymond J, Blankenship RE. 2003. Horizontal gene transfer in eukaryotic algal evolution. Proc Natl Acad Sci U S A 100:7419–7420. doi:10.1073/pnas.1533212100

Reidy M, Kumar S, Anderson DE, Masison DC. 2018. Dual Roles for Yeast Sti1/Hop in Regulating the Hsp90 Chaperone Cycle. Genetics 209:1139–1154. doi:10.1534/genetics.118.301178

Reis AC, Salis HM. 2020. An Automated Model Test System for Systematic Development and Improvement of Gene Expression Models. ACS Synth Biol 9:3145–3156. doi:10.1021/acssynbio.0c00394

Reißer S, Strandberg E, Steinbrecher T, Ulrich AS. 2014. 3D hydrophobic moment vectors as a tool to characterize the surface polarity of amphiphilic peptides. Biophys J 106:2385–2394. doi:10.1016/j.bpj.2014.04.020

Revell LJ. 2012. Phytools: An R package for phylogenetic comparative biology (and other things). Methods in ecology and evolution 217–223.

Revolution Analytics, Weston S. 2015a. doMC: Foreach Parallel Adaptor for ’parallel’.

Revolution Analytics, Weston S. 2015b. doParallel: Foreach Parallel Adaptor for the ’parallel’ Package.

Revolution Analytics, Weston S. 2015c. Foreach: Provides Foreach Looping Construct for R.

Revolution Analytics, Weston S. 2015d. Iterators: Provides Iterator Construct for R.

Richardson JS. 2000. Early ribbon drawings of proteins. Nature Structural Biology 7:624–625. doi:10.1038/77912

Ries F, Herkt C, Willmund F. 2020. Co-Translational Protein Folding and Sorting in Chloroplasts. Plants (Basel) 9:214. doi:10.3390/plants9020214

Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez J-C, Müller M. 2011. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC bioinformatics 12:77. doi:10.1186/1471-2105-12-77

Rodrigo-Brenni MC, Gutierrez E, Hegde RS. 2014. Cytosolic quality control of mislocalized proteins requires RNF126 recruitment to Bag6. Mol Cell 55:227–237. doi:10.1016/j.molcel.2014.05.025

Rogowitz BE, Kalvin AD. 2001. The "Which Blair project": A quick visual method for evaluating perceptual color mapsProceedings Visualization, 2001. VIS ’01. Presented at the VIS 2001. Visualization 2001. San Diego, CA, USA: IEEE. pp. 183–556. doi:10.1109/VISUAL.2001.964510

Röhl A, Rohrberg J, Buchner J. 2013. The chaperone Hsp90: Changing partners for demanding clients. Trends Biochem Sci 38:253–262. doi:10.1016/j.tibs.2013.02.003

Röhl A, Wengler D, Madl T, Lagleder S, Tippel F, Herrmann M, Hendrix J, Richter K, Hack G, Schmid AB, Kessler H, Lamb DC, Buchner J. 2015. Hsp90 regulates the dynamics of its cochaperone Sti1 and the transfer of Hsp70 between modules. Nat Commun 6:6655. doi:10.1038/ncomms7655

Rome ME, Chio US, Rao M, Gristick H, Shan S. 2014. Differential gradients of interaction affinities drive efficient targeting and recycling in the GET pathway. Proc Natl Acad Sci U S A 111:E4929–4935. doi:10.1073/pnas.1411284111

Rome ME, Rao M, Clemons WM, Shan S. 2013. Precise timing of ATPase activation drives targeting of tail-anchored proteins. Proc Natl Acad Sci U S A 110:7666–7671. doi:10.1073/pnas.1222054110

Roseman MA. 1988. Hydrophilicity of polar amino acid side-chains is markedly reduced by flanking peptide bonds. J Mol Biol 200:513–522. doi:10.1016/0022-2836(88)90540-2

Rosen BP, Weigel U, Karkaria C, Gangola P. 1988. Molecular characterization of a unique anion pump: The ArsA protein is an arsenite(antimonate)-stimulated ATPase. Prog Clin Biol Res 273:105–112.

RStudio Team. 2015. RStudio: Integrated Development Environment for R.

Russell RB, Barton GJ. 1992. Multiple protein sequence alignment from tertiary structure comparison: Assignment of global and residue confidence levels. Proteins 14:309–323. doi:10.1002/prot.340140216

Saeki Y, Sone T, Toh-e A, Yokosawa H. 2002. Identification of ubiquitin-like protein-binding subunits of the 26S proteasome. Biochem Biophys Res Commun 296:813–819. doi:10.1016/s0006-291x(02)02002-8

Saier MH, Reddy VS, Tsu BV, Ahmed MS, Li C, Moreno-Hagelsieb G. 2016. The transporter classification database (TCDB): Recent advances. Nucleic Acids Research 44:D372–379. doi:10.1093/nar/gkv1103

Saladi SM, Maggiolo AO, Radford K, Clemons WM. 2020. Structural biologists, let’s mind our colors (preprint). Biochemistry. doi:10.1101/2020.09.22.308593

Sarkar CA, Dodevski I, Kenig M, Dudli S, Mohr A, Hermans E, Plückthun A. 2008. Directed evolution of a G protein-coupled receptor for expression, stability, and binding selectivity. Proceedings of the National Academy of Sciences of the United States of America 105:14808–14813. doi:10.1073/pnas.0803103105

Schägger H. 2006. Tricine-SDS-PAGE. Nat Protoc 1:16–22. doi:10.1038/nprot.2006.4

Scheufler C, Brinker A, Bourenkov G, Pegoraro S, Moroder L, Bartunik H, Hartl FU, Moarefi I. 2000. Structure of TPR domain-peptide complexes: Critical elements in the assembly of the Hsp70-Hsp90 multichaperone machine. Cell 101:199–210. doi:10.1016/S0092-8674(00)80830-2

Schiffer M, Edmundson AB. 1967. Use of helical wheels to represent the structures of proteins and to identify segments with helical potential. Biophys J 7:121–135. doi:10.1016/S0006-3495(67)86579-2

Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, Tinevez J-Y, White DJ, Hartenstein V, Eliceiri K, Tomancak P, Cardona A. 2012. Fiji: An open-source platform for biological-image analysis. Nat Methods 9:676–682. doi:10.1038/nmeth.2019

Schlinkmann KM, Honegger A, Türeci E, Robison KE, Lipovšek D, Plückthun A. 2012. Critical features for biosynthesis, stability, and functionality of a G protein-coupled receptor uncovered by all-versus-all mutations. Proceedings of the National Academy of Sciences of the United States of America 109:9810–9815. doi:10.1073/pnas.1202107109

Schloerke B, Crowley J, Cook D, Briatte F, Marbach M, Thoen E, Elberg A, Larmarange J. 2016. GGally: Extension to ’Ggplot2’.

Schmid AB, Lagleder S, Gräwert MA, Röhl A, Hagn F, Wandinger SK, Cox MB, Demmer O, Richter K, Groll M, Kessler H, Buchner J. 2012. The architecture of functional modules in the Hsp90 co-chaperone Sti1/Hop. EMBO J 31:1506–1517. doi:10.1038/emboj.2011.472

Schneider CA, Rasband WS, Eliceiri KW. 2012. NIH Image to ImageJ: 25 years of image analysis. Nat Methods 9:671–675. doi:10.1038/nmeth.2089

Schopf FH, Biebl MM, Buchner J. 2017. The HSP90 chaperone machinery. Nat Rev Mol Cell Biol 18:345–360. doi:10.1038/nrm.2017.20

Schuldiner M, Metz J, Schmid V, Denic V, Rakwalska M, Schmitt HD, Schwappach B, Weissman JS. 2008. The GET complex mediates insertion of tail-anchored proteins into the ER membrane. Cell 134:634–645. doi:10.1016/j.cell.2008.06.025

Schuler GD, Epstein JA, Ohkawa H, Kans JA. 1996. Entrez: Molecular biology database and retrieval system. Methods in Enzymology 266:141–162.

Şentürk M, Lin G, Zuo Z, Mao D, Watson E, Mikos AG, Bellen HJ. 2019. Ubiquilins regulate autophagic flux through mTOR signalling and lysosomal acidification. Nat Cell Biol 21:384–396. doi:10.1038/s41556-019-0281-x

Seppälä S, Slusky JS, Lloris-Garcerá P, Rapp M, von Heijne G. 2010. Control of membrane protein topology by a single C-terminal residue. Science (New York, NY) 328:1698–1700. doi:10.1126/science.1188950

Serres MH, Kerr ARW, McCormack TJ, Riley M. 2009. Evolution by leaps: Gene duplication in bacteria. Biol Direct 4:46. doi:10.1186/1745-6150-4-46

Shan S-O. 2019. Guiding tail-anchored membrane proteins to the endoplasmic reticulum in a chaperone cascade. J Biol Chem 294:16577–16586. doi:10.1074/jbc.REV119.006197

Shao S, Hegde RS. 2011a. A calmodulin-dependent translocation pathway for small secretory proteins. Cell 147:1576–1588. doi:10.1016/j.cell.2011.11.048

Shao S, Hegde RS. 2011b. Membrane protein insertion at the endoplasmic reticulum. Annu Rev Cell Dev Biol 27:25–56. doi:10.1146/annurev-cellbio-092910-154125

Shao S, Rodrigo-Brenni MC, Kivlen MH, Hegde RS. 2017. Mechanistic basis for a molecular triage reaction. Science 355:298–302. doi:10.1126/science.aah6130

Shi T, Falkowski PG. 2008. Genome evolution in cyanobacteria: The stable core and the variable shell. Proc Natl Acad Sci U S A 105:2510–2515. doi:10.1073/pnas.0711165105

Shindyalov IN, Bourne PE. 1998. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng 11:739–747. doi:10.1093/protein/11.9.739

Simão FA, Waterhouse RM, Ioannidis P, Kriventseva EV, Zdobnov EM. 2015. BUSCO: Assessing genome assembly and annotation completeness with single-copy orthologs. Bioinformatics 31:3210–3212. doi:10.1093/bioinformatics/btv351

Simon AC, Simpson PJ, Goldstone RM, Krysztofinska EM, Murray JW, High S, Isaacson RL. 2013. Structure of the Sgt2/Get5 complex provides insights into GET-mediated targeting of tail-anchored membrane proteins. Proc Natl Acad Sci U S A 110:1327–1332. doi:10.1073/pnas.1207518110

Sjores S. 2020. The following colour schemes have now been implemented.

Slabinski L, Jaroszewski L, Rodrigues APC, Rychlewski L, Wilson IA, Lesley SA, Godzik A. 2007a. The challenge of protein structure determination–lessons from structural genomics. Protein Science: A Publication of the Protein Society 16:2472–2482. doi:10.1110/ps.073037907

Slabinski L, Jaroszewski L, Rychlewski L, Wilson IA, Lesley SA, Godzik A. 2007b. XtalPred: A web server for prediction of protein crystallizability. Bioinformatics (Oxford, England) 23:3403–3405. doi:10.1093/bioinformatics/btm477

Smith NJ, Futrell R, Walt SVD, Mansencal T, TFiFiE, Betts E, Cgohlke, Dieterle B. 2018. Njsmith/Colorspacious V1.1.2. doi:10.5281/ZENODO.1214904

Smith N, van der Walt S. 2015. A Better Default Colormap for Matplotlib.

Spatzal T, Aksoyoglu M, Zhang L, Andrade SLA, Schleicher E, Weber S, Rees DC, Einsle O. 2011. Evidence for Interstitial Carbon in Nitrogenase FeMo Cofactor. Science 334:940–940. doi:10.1126/science.1214025

Srivastava R, Zalisko BE, Keenan RJ, Howell SH. 2017. The GET System Inserts the Tail-Anchored Protein, SYP72, into Endoplasmic Reticulum Membranes. Plant Physiol 173:1137–1145. doi:10.1104/pp.16.00928

Stamatakis A. 2014. RAxML version 8: A tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 30:1312–1313. doi:10.1093/bioinformatics/btu033

Stefanovic S, Hegde RS. 2007. Identification of a targeting factor for posttranslational membrane protein insertion into the ER. Cell 128:1147–1159. doi:10.1016/j.cell.2007.01.036

Stefer S, Reitz S, Wang F, Wild K, Pang Y-Y, Schwarz D, Bomke J, Hein C, Löhr F, Bernhard F, Denic V, Dötsch V, Sinning I. 2011. Structural basis for tail-anchored membrane protein biogenesis by the Get3-receptor complex. Science 333:758–762. doi:10.1126/science.1207125

Steinegger M, Söding J. 2018. Clustering huge protein sequence sets in linear time. Nat Commun 9:2542. doi:10.1038/s41467-018-04964-5

Stringer C, Wang T, Michaelos M, Pachitariu M. 2021. Cellpose: A generalist algorithm for cellular segmentation. Nat Methods 18:100–106. doi:10.1038/s41592-020-01018-x

Studier FW. 2005. Protein production by auto-induction in high density shaking cultures. Protein Expr Purif 41:207–234. doi:10.1016/j.pep.2005.01.016

Subudhi I, Shorter J. 2018. Ubiquilin 2: Shuttling Clients Out of Phase? Mol Cell 69:919–921. doi:10.1016/j.molcel.2018.02.030

Suloway CJM, Chartron JW, Zaslaver M, Clemons WM. 2009. Model for eukaryotic tail-anchored protein binding based on the structure of Get3. Proc Natl Acad Sci U S A 106:14849–14854. doi:10.1073/pnas.0907522106

Suloway CJM, Rome ME, Clemons WM. 2012. Tail-anchor targeting by a Get3 tetramer: The structure of an archaeal homologue. EMBO J 31:707–719. doi:10.1038/emboj.2011.433

Surade S, Klein M, Stolt-Bergner PC, Muenke C, Roy A, Michel H. 2006. Comparative analysis and "expression space" coverage of the production of prokaryotic membrane proteins for structural genomics. Protein Science 15:2178–2189. doi:10.1110/ps.062312706

Swets JA, Dawes RM, Monahan J. 2000. Better decisions through science. Sci Am 283:82–87. doi:10.1038/scientificamerican1000-82

Szakonyi G, Leng D, Ma P, Bettaney KE, Saidijam M, Ward A, Zibaei S, Gardiner AT, Cogdell RJ, Butaye P, Kolsto A-B, O’reilly J, Hope RJ, Rutherford NG, Hoyle CJ, Henderson PJF. 2007. A genomic strategy for cloning, expressing and purifying efflux proteins of the major facilitator superfamily. The Journal of Antimicrobial Chemotherapy 59:1265–1270. doi:10.1093/jac/dkm036

Tange O. 2011. GNU parallel - the command-line power tool. ;login: The USENIX Magazine 36:42–47. doi:10.5281/zenodo.16303

Ten Eyck LF. 1973. Crystallographic fast Fourier transforms. Acta Cryst A 29:183–191. doi:10.1107/S0567739473000458

The UniProt Consortium. 2017. UniProt: The universal protein knowledgebase. Nucleic Acids Res 45:D158–D169. doi:10.1093/nar/gkw1099

Thompson JD, Gibson TJ, Plewniak F, Jeanmougin F, Higgins DG. 1997. The CLUSTAL_X windows interface: Flexible strategies for multiple sequence alignment aided by quality analysis tools. Nucleic Acids Res 25:4876–4882. doi:10.1093/nar/25.24.4876

Tidow H, Nissen P. 2013. Structural diversity of calmodulin binding to its target sites. FEBS J 280:5551–5565. doi:10.1111/febs.12296

Tomb JF, White O, Kerlavage AR, Clayton RA, Sutton GG, Fleischmann RD, Ketchum KA, Klenk HP, Gill S, Dougherty BA, Nelson K, Quackenbush J, Zhou L, Kirkness EF, Peterson S, Loftus B, Richardson D, Dodson R, Khalak HG, Glodek A, McKenney K, Fitzegerald LM, Lee N, Adams MD, Hickey EK, Berg DE, Gocayne JD, Utterback TR, Peterson JD, Kelley JM, Cotton MD, Weidman JM, Fujii C, Bowman C, Watthey L, Wallin E, Hayes WS, Borodovsky M, Karp PD, Smith HO, Fraser CM, Venter JC. 1997. The complete genome sequence of the gastric pathogen Helicobacter pylori. Nature 388:539–547. doi:10.1038/41483

Towns J, Cockerill T, Dahan M, Foster I, Gaither K, Grimshaw A, Hazlewood V, Lathrop S, Lifka D, Peterson GD, Roskies R, Scott JR, Wilkens-Diehr N. 2014. XSEDE: Accelerating scientific discovery. Computing in Science & Engineering 16:62–74. doi:10.1109/MCSE.2014.80

Trempe J-F, Šašková KG, Sivá M, Ratcliffe CDH, Veverka V, Hoegl A, Ménade M, Feng X, Shenker S, Svoboda M, Kožíšek M, Konvalinka J, Gehring K. 2016. Structural studies of the yeast DNA damage-inducible protein Ddi1 reveal domain architecture of this eukaryotic protein family. Sci Rep 6:33671. doi:10.1038/srep33671

Trotta AP, Need EF, Selth LA, Chopra S, Pinnock CB, Leach DA, Coetzee GA, Butler LM, Tilley WD, Buchanan G. 2013. Knockdown of the cochaperone SGTA results in the suppression of androgen and PI3K/Akt signaling and inhibition of prostate cancer cell proliferation. Int J Cancer 133:2812–2823. doi:10.1002/ijc.28310

Tsirigos KD, Peters C, Shu N, Käll L, Elofsson A. 2015. The TOPCONS web server for consensus prediction of membrane protein topology and signal peptides. Nucleic Acids Res 43:W401–407. doi:10.1093/nar/gkv485

Tsochantaridis I, Joachims T, Hofmann T, Altun Y. 2005. Large margin methods for structured and interdependent output variables. Journal of Machine Learning Research 6:1453–1484.

UniProt Consortium. 2021. UniProt: The universal protein knowledgebase in 2021. Nucleic Acids Res 49:D480–D489. doi:10.1093/nar/gkaa1100

UniProt Consortium. 2012. Reorganizing the protein space at the Universal Protein Resource (UniProt). Nucleic Acids Res 40:D71–75. doi:10.1093/nar/gkr981

Van den Berg B, Clemons WM, Collinson I, Modis Y, Hartmann E, Harrison SC, Rapoport TA. 2004. X-ray structure of a protein-conducting channel. Nature 427:36–44. doi:10.1038/nature02218

van der Walt S, Colbert SC, Varoquaux G. 2011. The NumPy array: A structure for efficient numerical computation. Computing in Science & Engineering 13:22–30. doi:10.1109/MCSE.2011.37

Van Lehn RC, Zhang B, Miller TF. 2015. Regulation of multispanning membrane protein topology via post-translational annealing. Elife 4. doi:10.7554/eLife.08697

Van Rossum G, Drake Jr FL. 1995. Python reference manual. Centrum voor Wiskunde en Informatica Amsterdam.

Vida TA, Emr SD. 1995. A new vital stain for visualizing vacuolar membrane dynamics and endocytosis in yeast. J Cell Biol 128:779–792. doi:10.1083/jcb.128.5.779

Vilardi F, Lorenz H, Dobberstein B. 2011. WRB is the receptor for TRC40/Asna1-mediated insertion of tail-anchored proteins into the ER membrane. J Cell Sci 124:1301–1307. doi:10.1242/jcs.084277

Voorhees RM, Hegde RS. 2015. Structures of the scanning and engaged states of the mammalian SRP-ribosome complex. Elife 4:e07975. doi:10.7554/eLife.07975

Wade SL, Auble DT. 2010. The Rad23 ubiquitin receptor, the proteasome and functional specificity in transcriptional control. Transcription 1:22–26. doi:10.4161/trns.1.1.12201

Wagner S, Klepsch MM, Schlegel S, Appel A, Draheim R, Tarry M, Högbom M, van Wijk KJ, Slotboom DJ, Persson JO, de Gier J-W. 2008. Tuning Escherichia coli for membrane protein overexpression. Proceedings of the National Academy of Sciences of the United States of America 105:14371–14376. doi:10.1073/pnas.0804090105

Waheed AA, MacDonald S, Khan M, Mounts M, Swiderski M, Xu Y, Ye Y, Freed EO. 2016. The Vpu-interacting Protein SGTA Regulates Expression of a Non-glycosylated Tetherin Species. Sci Rep 6:24934. doi:10.1038/srep24934

Wallner B, Elofsson A. 2006. Identification of correct regions in protein models using structural, alignment, and consensus information. Protein Sci 15:900–913. doi:10.1110/ps.051799606

Wang F, Brown EC, Mak G, Zhuang J, Denic V. 2010. A chaperone cascade sorts proteins for posttranslational membrane insertion into the endoplasmic reticulum. Mol Cell 40:159–171. doi:10.1016/j.molcel.2010.08.038

Wang F, Whynot A, Tung M, Denic V. 2011. The mechanism of tail-anchored protein insertion into the ER membrane. Mol Cell 43:738–750. doi:10.1016/j.molcel.2011.07.020

Wang H, Feng L, Zhang Z, Webb GI, Lin D, Song J. 2016. Crysalis: An integrated server for computational analysis and design of protein crystallization. Scientific Reports 6:21383. doi:10.1038/srep21383

Wang H, Zhang Q, Zhu D. 2003. hSGT interacts with the N-terminal region of myostatin. Biochem Biophys Res Commun 311:877–883. doi:10.1016/j.bbrc.2003.10.080

Wang L-G, Lam TT-Y, Xu S, Dai Z, Zhou L, Feng T, Guo P, Dunn CW, Jones BR, Bradley T, Zhu H, Guan Y, Jiang Y, Yu G. 2020. Treeio: An R Package for Phylogenetic Tree Input and Output with Richly Annotated and Associated Data. Mol Biol Evol 37:599–603. doi:10.1093/molbev/msz240

Ward N, Moreno-Hagelsieb G. 2014. Quickly finding orthologs as reciprocal best hits with BLAT, LAST, and UBLAST: How much do we miss? PLoS One 9:e101850. doi:10.1371/journal.pone.0101850

Waterhouse AM, Procter JB, Martin DMA, Clamp M, Barton GJ. 2009. Jalview Version 2–a multiple sequence alignment editor and analysis workbench. Bioinformatics 25:1189–1191. doi:10.1093/bioinformatics/btp033

Watkins JF, Sung P, Prakash L, Prakash S. 1993. The Saccharomyces cerevisiae DNA repair gene RAD23 encodes a nuclear protein containing a ubiquitin-like domain required for biological function. Mol Cell Biol 13:7757–7765. doi:10.1128/mcb.13.12.7757-7765.1993

Wattenberg B, Lithgow T. 2001. Targeting of C-terminal (tail)-anchored proteins: Understanding how cytoplasmic activities are anchored to intracellular membranes. Traffic 2:66–71. doi:10.1034/j.1600-0854.2001.20108.x

Webb B, Sali A. 2016. Comparative Protein Structure Modeling Using MODELLER. Curr Protoc Bioinformatics 54:5.6.1–5.6.37. doi:10.1002/cpbi.3

Weihs C, Ligges U, Luebke K, Raabe N. 2005. klaR analyzing german business cycles In: Baier D, Decker R, Schmidt-Thieme L, editors. Data Analysis and Decision Support. Berlin/Heidelberg: Springer-Verlag. pp. 335–343.

Weill U, Yofe I, Sass E, Stynen B, Davidi D, Natarajan J, Ben-Menachem R, Avihou Z, Goldman O, Harpaz N, Chuartzman S, Kniazev K, Knoblach B, Laborenz J, Boos F, Kowarzyk J, Ben-Dor S, Zalckvar E, Herrmann JM, Rachubinski RA, Pines O, Rapaport D, Michnick SW, Levy ED, Schuldiner M. 2018. Genome-wide SWAp-Tag yeast libraries for proteome exploration. Nat Methods 15:617–622. doi:10.1038/s41592-018-0044-9

Weinert K. 2014. Datamart: Unified access to your data sources.

Weisman CM, Murray AW, Eddy SR. 2020. Many, but not all, lineage-specific genes can be explained by homology detection failure. PLoS Biol 18:e3000862. doi:10.1371/journal.pbio.3000862

Wickham H. n.d. Multidplyr: Partitioned data frames for ’dplyr’.

Wickham H. 2016. Ggplot2: Elegant graphics for data analysis. Springer-Verlag New York.

Wickham H. 2015. Scales: Scale functions for visualization.

Wickham H. 2011. The split-apply-combine strategy for data analysis. Journal of Statistical Software 40:1–29.

Wickham H, Averick M, Bryan J, Chang W, McGowan LD, François R, Grolemund G, Hayes A, Henry L, Hester J, others. 2019. Welcome to the tidyverse. Journal of open source software 4:1686.

Wickham H, Danenberg P, Eugster M. 2015. Roxygen2: In-source documentation for R.

Wickham H, Francois R. 2015. Dplyr: A grammar of data manipulation.

Wilke CO. 2015. Cowplot: Streamlined plot theme and plot annotations for ’Ggplot2’.

Wimley WC, Creamer TP, White SH. 1996. Solvation energies of amino acid side chains and backbone in a family of host-guest pentapeptides. Biochemistry 35:5109–5124. doi:10.1021/bi9600153

Winkler K-HA, Norman ML. 1986. Munacolor: Understanding high-resolution gas dynamical simulations through color graphics. Astrophysical radiation hydrodynamics 223–243.

Winn MD, Ballard CC, Cowtan KD, Dodson EJ, Emsley P, Evans PR, Keegan RM, Krissinel EB, Leslie AGW, McCoy A, McNicholas SJ, Murshudov GN, Pannu NS, Potterton EA, Powell HR, Read RJ, Vagin A, Wilson KS. 2011. Overview of the CCP4 suite and current developments. Acta Crystallogr D Biol Crystallogr 67:235–242. doi:10.1107/S0907444910045749

Winnefeld M, Grewenig A, Schnölzer M, Spring H, Knoch TA, Gan EC, Rommelaere J, Cziepluch C. 2006. Human SGT interacts with Bag-6/Bat-3/Scythe and cells with reduced levels of either protein display persistence of few misaligned chromosomes and mitotic arrest. Exp Cell Res 312:2500–2514. doi:10.1016/j.yexcr.2006.04.020

Wunderley L, Leznicki P, Payapilly A, High S. 2014. SGTA regulates the cytosolic quality control of hydrophobic substrates. J Cell Sci 127:4728–4739. doi:10.1242/jcs.155648

Xie Y. 2014. Knitr: A comprehensive tool for reproducible research in R In: Stodden V, Leisch F, Peng RD, editors. Implementing Reproducible Computational Research. Chapman and Hall/CRC.

Xing S, Mehlhorn DG, Wallmeroth N, Asseck LY, Kar R, Voss A, Denninger P, Schmidt VAF, Schwarzländer M, Stierhof Y-D, Grossmann G, Grefen C. 2017. Loss of GET pathway orthologs in Arabidopsis thaliana causes root hair growth defects and affects SNARE abundance. Proc Natl Acad Sci U S A 114:E1544–E1553. doi:10.1073/pnas.1619525114

Xu D, Zhang Y. 2012. Ab initio protein structure assembly using continuous structure fragments and optimized knowledge-based force field. Proteins 80:1715–1735. doi:10.1002/prot.24065

Xu Y, Cai M, Yang Y, Huang L, Ye Y. 2012. SGTA recognizes a noncanonical ubiquitin-like domain in the Bag6-Ubl4A-Trc35 complex to promote endoplasmic reticulum-associated degradation. Cell Rep 2:1633–1644. doi:10.1016/j.celrep.2012.11.010

Xu Y, Liu Y, Lee J, Ye Y. 2013. A ubiquitin-like domain recruits an oligomeric chaperone to a retrotranslocation complex in endoplasmic reticulum-associated degradation. J Biol Chem 288:18068–18076. doi:10.1074/jbc.M112.449199

Yamamoto Y, Sakisaka T. 2012. Molecular machinery for insertion of tail-anchored membrane proteins into the endoplasmic reticulum membrane in mammalian cells. Mol Cell 48:387–397. doi:10.1016/j.molcel.2012.08.028

Yang J, Anishchenko I, Park H, Peng Z, Ovchinnikov S, Baker D. 2020. Improved protein structure prediction using predicted interresidue orientations. Proc Natl Acad Sci U S A 117:1496–1503. doi:10.1073/pnas.1914677117

Yang J, Yan R, Roy A, Xu D, Poisson J, Zhang Y. 2015. The I-TASSER Suite: Protein structure and function prediction. Nat Methods 12:7–8. doi:10.1038/nmeth.3213

Yang ZR, Thomson R, McNeil P, Esnouf RM. 2005. RONN: The bio-basis function neural network technique applied to the detection of natively disordered regions in proteins. Bioinformatics 21:3369–3376. doi:10.1093/bioinformatics/bti534

Yariv B, Yariv E, Kessel A, Masrati G, Chorin AB, Martz E, Mayrose I, Pupko T, Ben-Tal N. 2023. Using evolutionary data to make sense of macromolecules with a “face-lifted” ConSurf. Protein Science 32:e4582. doi:10.1002/pro.4582

Yu G. 2022. Data integration, manipulation and visualization of phylogenetic trees. CRC Press.

Yu G. 2020. Using ggtree to Visualize Data on Tree-Like Structures. Curr Protoc Bioinformatics 69:e96. doi:10.1002/cpbi.96

Yuan S, Qin W, Riordan CR, McSwiggin H, Zheng H, Yan W. 2015. Ubqln3, a testis-specific gene, is dispensable for embryonic development and spermatogenesis in mice. Mol Reprod Dev 82:266–267. doi:10.1002/mrd.22475

Zadeh JN, Steenberg CD, Bois JS, Wolfe BR, Pierce MB, Khan AR, Dirks RM, Pierce NA. 2011. NUPACK: Analysis and design of nucleic acid systems. Journal of Computational Chemistry 32:170–173. doi:10.1002/jcc.21596

Zanata SM, Lopes MH, Mercadante AF, Hajj GNM, Chiarini LB, Nomizo R, Freitas ARO, Cabral ALB, Lee KS, Juliano MA, de Oliveira E, Jachieri SG, Burlingame A, Huang L, Linden R, Brentani RR, Martins VR. 2002. Stress-inducible protein 1 is a cell surface ligand for cellular prion that triggers neuroprotection. EMBO J 21:3307–3316. doi:10.1093/emboj/cdf325

Zeytuni N, Zarivach R. 2012. Structural and functional discussion of the tetra-trico-peptide repeat, a protein interaction module. Structure 20:397–405. doi:10.1016/j.str.2012.01.006

Zhang D, Raasi S, Fushman D. 2008. Affinity makes the difference: Nonselective interaction of the UBA domain of Ubiquilin-1 with monomeric ubiquitin and polyubiquitin chains. J Mol Biol 377:162–180. doi:10.1016/j.jmb.2007.12.029

Zhao G, London E. 2006. An amino acid "transmembrane tendency" scale that approaches the theoretical limit to accuracy for prediction of transmembrane helices: Relationship to biological hydrophobicity. Protein Sci 15:1987–2001. doi:10.1110/ps.062286306

Zhaxybayeva O, Gogarten JP, Charlebois RL, Doolittle WF, Papke RT. 2006. Phylogenetic analyses of cyanobacterial genomes: Quantification of horizontal gene transfer events. Genome Res 16:1099–1108. doi:10.1101/gr.5322306

Zhou J, Rudd KE. 2013. EcoGene 3.0. Nucleic Acids Research 41:D613–624. doi:10.1093/nar/gks1235

Zhou T, Radaev S, Rosen BP, Gatti DL. 2000. Structure of the ArsA ATPase: The catalytic subunit of a heavy metal resistance pump. EMBO J 19:4838–4845. doi:10.1093/emboj/19.17.4838

Zientara-Rytter K, Subramani S. 2019. The Roles of Ubiquitin-Binding Protein Shuttles in the Degradative Fate of Ubiquitinated Proteins in the Ubiquitin-Proteasome System and Autophagy. Cells 8:40. doi:10.3390/cells8010040

Zimorski V, Ku C, Martin WF, Gould SB. 2014. Endosymbiotic theory for organelle origins. Curr Opin Microbiol 22:38–48. doi:10.1016/j.mib.2014.09.008

Zopf D, Bernstein HD, Johnson AE, Walter P. 1990. The methionine-rich domain of the 54 kd protein subunit of the signal recognition particle contains an RNA binding site and can be crosslinked to a signal sequence. EMBO J 9:4511–4517. doi:10.1002/j.1460-2075.1990.tb07902.x